Модели системы с распределенными параметрами

Рассмотрим более общие случаи, в которых параметры каждой точки тела или среды зависят от параметров соседних точек. Описываются такие процессы нестационарными дифференциальными уравнениями в частных производных с краевыми условиями.

Численное решения таких задач целесообразно осуществить методом конечных разностей, вводя дискретные переменные t,x,y,…,t, т.е. описывая время процесса: t=kDt, а координаты пространственной сетки Dx´Dy´…: x=iDx, y=iDy,….

Откуда после замены производных конечными разностями для параметров t

;

;

; …

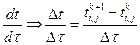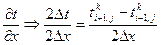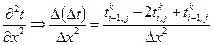В результате подстановки в дифференциальное уравнение получим выражение для расчета параметра t в i, j-м узле сетки в (k+1)-й момент времени по известным для k-го момента параметрам окружающих узлов сетки:

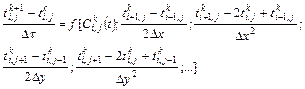(13.1)

где значения переменных 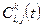принимаются в соответствии с параметрами центрального узла сетки 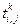в k-й момент времени.

Уравнение типа (13.1) решается в явном виде относительно 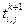, что позволяет последовательно обходя все узлы сетки по столбцам и строкам сеточного поля, определить распределение параметра t через время Dt, 2Dt,…,kDt от заданного в начальный момент t=0.

На границах тела, где уравнение (13.1) не может быть использовано, так как граничные точки не окружены со всех сторон узлами сетки, используется разностная форма граничных условий

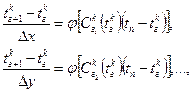(13.2)

где 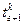- параметр соседней с граничной внутренней точки тела, 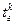- параметр граничной точки, 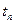- значения параметра окружающей среды, 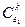, , 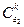… - значения переменных, принимающиеся в зависимости от параметра 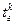в k-й момент времени

Описанное в (13.1) и (13.2) приближение модели к реальному процессу по геометрии изделия, по действительной зависимости свойств от изменяющихся параметров с течением времени, позволяют вплотную подойти к построению имитационной модели. При необходимости в подобного рода моделях могут быть приняты в расчет особенности конкретных технологических процессов воспроизводящие ход реального процесса во времени в различных точках рабочей зоны.

Лекция №14