И дисперсионного анализа

Для технологических экспериментов, характерны статистические объекты исследований, в которых имеют место стохастические или корреляционные взаимосвязи между параметрами и факторами. Получить математическую модель технологического процесса- значит найти математическое описание этих взаимосвязей.

В задачу корреляционного, регрессионного и дисперсионного анализа входит получение на основании экспериментальных данных математической модели процесса и ее анализ. Методы корреляционного и регрессионного анализа применимы только для таких параметров, которые при изучении физической природы объекта являются взаимосвязанными.

На первом этапе обычно оценивают степень тесноты взаимосвязи значений функции отклика с одной или несколькими независимыми переменными. В первом случае используется коэффициент парной корреляции r_yx, во втором - коэффициент множественной корреляции .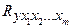

Коэффициент парной корреляции:

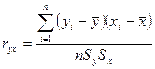(14.1)

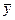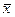где n - объем выборки, и - средние арифметические значения y_i и x_i в рассматриваемой выборке, S_y и S_x их средние квадратические отклонения.

Коэффициент множественной корреляции с использованием метода определителей находится по формуле

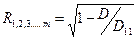(14.2)

где m - число независимых переменных, D - определитель, составленный из всех коэффициентов парной корреляции, D₁₁- определитель, получающийся из D исключением левого столбца и верхней строки.

;

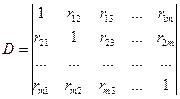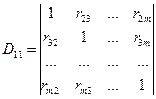
Значения r_yx (14.1) и 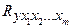(14.2) находятся в пределах от -1 до +1. Если они достоверны, т.е. существенно отличаются от 0, значит между исследуемыми факторами имеется линейная корреляционная зависимость. В противном случае эта зависимость отсутствует, либо является существенно нелинейной. В результате корреляционным анализом подтверждается наличие взаимосвязей между исследуемыми факторами.

На следующем этапе обработки экспериментальных данных с помощью регрессионного анализа выбирают модель, в наилучшей степени описывающую указанные взаимосвязи. Уравнение, по которому могут быть найдены числовые значения выборочных средних функций отклика при соответствующих значениях независимых переменных называется уравнением регрессии. В общем случае оно может быть записано в виде

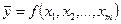(14.3)

При аппроксимации неизвестных функций отклика (14.3) в математической статистике часто используют полиномиальные модели, а наиболее часто - простейшие из них - квадратичные.

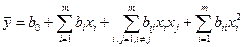(14.4)

где b₀, b_i, b_ij, b_ii – коэффициенты регрессии.

С позиций статистики полиномиальная модель (14.4) удобна тем, что позволяет увеличить степень точности аппроксимации за счет повышения порядка полинома.

При определении параметров уравнения регрессии все переменные и соотношения между ними выгодно выражать в стандартизированном масштабе. Значения переменных в стандартизированном масштабе определяются по формуле:

,

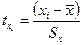где x_i - значения переменных в натуральном масштабе, S_x – их среднеквадратичные отклонения от среднеарифметического значения .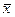

Лекция №15