Модели системы с сосредоточенными параметрами

При возникновении трудностей в использовании аналитической модели, для получения которой требуется принимать допущения о постоянстве параметров дифференциальных уравнений (7.1)-(9.8) и (10.1)-(11.4), во многих случаях целесообразно решать задачи с произвольным законом изменения параметров, применяя численные решения.

Обычно для решения дифференциальных уравнений используют разностные методы. Исходное дифференциальное уравнение, общий вид которого может быть представлен выражением

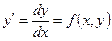, (12.1)

для численного решения преобразуется к разностному виду введением дискретных переменных (x₀,x₁,x₂,…,x_n) и (y₀,y₁,y₂,…,y_n). Обычно дают равномерное приращение независимой переменной Dx, откуда x_i=x₀+iDx, где i=0,1,2,...,n. Тогда (12.1) в разностной форме

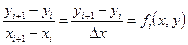
откуда

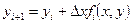(12.2)

В результате (12.2) позволяет по известному значению y_i и f_i(x,y) на предыдущем i-том шаге по x найти y на последующем (i+1)-ом шаге.

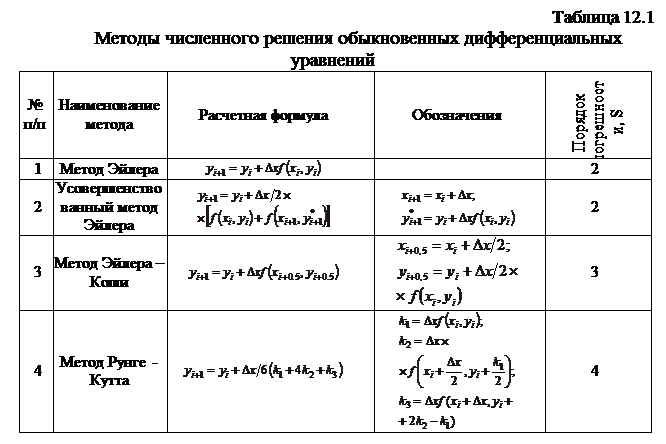
Чтобы осуществить этот процесс вычислений вплоть до n-го шага надо задать начальное y(x₀)=y₀. Вид функции f_i(x,y) зависит от принятого метода вычисления производной (табл.12.1).

В простейшем случае, реализующем метод Эйлера, задают f_i(x,y)= f(x_i,y_i), т.е. экстраполируют производную на целый шаг Dx вперед, вычислив ее значение в предыдущей точке. При использовании методов повышенной точности Эйлера-Коши, Рунге-Кутта и др., погрешность решения может быть существенно снижена при сокращении времени расчетов.

Для проверки расчетов при численном интегрировании уравнения (12.1), необходимо задать величину шага Dx, от которого зависят погрешность вычислений dy и затраты времени на расчеты. Для оценки погрешности, вносимой численным методом решения задачи, используют два приема.

При втором, сопоставляют результаты повторного решения задачи с последовательно уменьшаемой величиной шага Dx. Если произвести вычисления, изменив Dx, в два раза, то для оценки dy можно воспользоваться приближенной формулой Рунге:

,

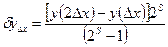где y(2Dx) и y(Dx) - расчетные значения полученные соответственно с шагом 2Dx и Dx, S - порядок погрешности, присущий выбранному методу (табл.12.1).

При уменьшении шага Dx, расчетные зависимости y(x) сxодятся к точному решению. Во многих случаях желательно предусмотреть автоматический выбор шага Dx, по оценке погрешности получаемого результата. В этих случаях сравнивают погрешность с заданной предельной ошибкой dy_max и если dy>dy_max повторяют вычисления с уменьшенным шагом Dx^*=a(Dx), в котором обычно a=0,8…0,9.

После устранения вычислительной погрешности, можно приступать к оценке адекватности модели, так как остаточная погрешность связана только с погрешностями физической модели и ее математической реализации.

Лекция №13