Условия применимости статистического анализа

Статистическое уравнение адекватно описывает результаты опытов, если квадратическое отклонение от экспериментальных данных 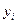значений зависимой переменной 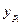, рассчитанной по уравнению регрессии, обусловлено только ошибкой воспроизведения (т.е. случайным характером этого параметра).

Применение корреляционного и регрессионного анализа правомерно и эффективно при соблюдении ряда условий.

1. Параметр оптимизации y - случайная величина с нормальным законом распределения.

2. Дисперсия 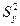не зависит от абсолютных значений величины y и остается постоянной и однородной при различных наблюдениях y.

3. Значения независимых переменных x₁, x₂,…,x_m изменяются с пренебрежимо малыми ошибками по сравнению с ошибкой в определении y.

4. Переменные x₁, x₂,…,x_m линейно независимы.

5. Процесс изменения зависимой переменной y является стационарным и случайным.

6. Экспериментальные данные получены из ряда независимых испытаний и образуют случайную выборку из данной генеральной совокупности.

Рассмотрим проверку выполнения этих условий.

1. Соответствие y нормальному закону распределения устанавливается либо по большим выборкам с помощью критериев Пирсона или Колмогорова, либо на основании анализа природы величины y.

2. Для оценки однородности дисперсии 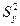проводят параллельные опыты в различных точках матрицы плана (т.е. при различных значениях x₁, x₂,…,x_m)

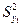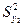Если сравниваются два значения и при различных числах степеней их свободы f (f=N-1, N -число параллельных опытов или объем выборки) то используется критерий Фишера, рассчитываемый как отношение большей дисперсии к меньшей

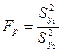, где 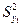> 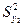, (15.1)

Если наблюдаемое значение Fp (15.1) меньше критического F_кр для соответствующих чисел степеней свободы и принятого уровня значимости, то опыты считаются воспроизводимыми, а дисперсии однородными.

Однородность ряда дисперсий при одинаковом числе опытов (для определения каждой из них) оценивают с помощью критерия Кохрена - отношения максимальной дисперсии к сумме всех дисперсий ряда:

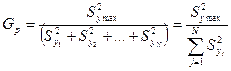, (15.2)

где N-число параллельных опытов или различных выборок. Дисперсии однородны, если расчетное значение G_p (15.2), не превышает критического G_кр.

При неравном числе степеней свободы для каждой из дисперсий ряда их однородность проверяют с помощью критерия Бартлета. Вначале определяют средневзвешенную дисперсию

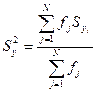, (15.3)

а затем вычисляют

;

;

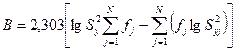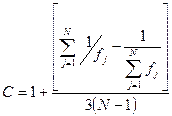где f_j=n_j-1, n_j - объем j-й выборки. В случае, когда все 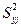соответствуют одной генеральной дисперсии, отношение В/С распределено аналогично критерию Пирсона c² с N-1 степенями свободы. Это значит, что при В/С£ 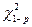, данном числе степеней свободы N-1 и заданном уровне значимости р дисперсии однородны.

3. Воспроизводимость опытов и однородность дисперсий достигается, когда выявлены и устранены источники нестабильности эксперимента, а также с помощью более точных средств и методов измерений.

Проверку достаточной точности измерения значений независимых переменных можно произвести, сопоставив ее с диапазоном изменения последних. Считается, что ошибки определения независимых переменных не должны превышать 5…7% интервала их варьирования. Ошибки в определении значений зависимой переменной не влияют столь значительно на точность регрессионного анализа и могут составить до 30% интервала варьирования.

4. Отсутствие коррелированности независимых переменных проверяется расчетом парных коэффициентов корреляции между ними.

5. Случайные процессы называют стационарными в том случае, когда основные характеристики процесса (математическое ожидание, дисперсия и др.) постоянны или однородны во времени. Поскольку при пассивном эксперименте свойства процесса определяются по одной представительной выборке, распространять полученные результаты на весь процесс можно лишь при условии его стационарности.

Проверка стационарности процесса производится в следующем порядке.

По результатам измерения параметра строится случайная последовательность его значений, соответствующая порядку проведения измерений. Полученную реализацию разбивают на несколько (5…10) равных отрезков, для каждого отрезка устанавливают дисперсию 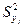и с помощью критерия Кохрена (15.2) определяют являются ли значения 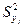на каждом из отрезков оценками одной и той же генеральной дисперсии s².

Затем на каждом отрезке проводится сравнение среднеарифметических 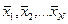, соответствующих выборочным дисперсиям 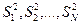, числам степеней свободы f₁, f₂,…, f_N (f_j=n_j-1, где n_j - объем соответствующей выборки). Всем выборкам соответствует генеральная дисперсия s², в качестве оценки которой, можно взять средневзвешенную дисперсию 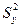(15.3).

Чтобы гипотеза о равенстве всех генеральных средних была справедлива, должно соблюдаться условие:

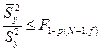, в котором ,

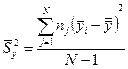где 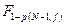- табличное значение критерия Фишера, 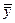-общее среднее всех элементов, отрезков, при объединении их в одну выборку

6. Проверку гипотезы о случайности выборки, необходимую при пассивном эксперименте, можно произвести методом последовательных разностей.

По значениям x_i выборки, расположенным в последовательности их наблюдения (x₁, x₂,…, x_n), образуется n-1 разностей между соседними членами: a₁= x₂- x₁, a₂= x₃- x₂,…, a_n-1= x_n- x_n-1.

Для оценки случайности выборки используется критерий 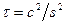, в котором:

;

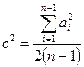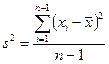
Если t<t_q, где t_q - критическое значение при уровне значимости q, то гипотеза о случайности выборки верна.

Лекция №16