Выбор параметров статистической модели

Параметром y статистической модели может быть только такая выходная переменная, которая поддается измерению с достаточной точностью и однозначно зависит от исследуемых факторов, являясь чувствительной к их изменениям. Важно, чтобы число параметров было минимальным, а в случае построения оптимизационной модели надо свести задачу к однопараметрической. Однако в большинстве случаев исследуемый процесс характеризуется целым набором разноплановых выходных параметров.

Для отбора наиболее важных параметров может быть использовано априорное ранжирование, а также анализ взаимной корреляции между параметрами с целью выявления сильно коррелированных параметров, не являющихся независимыми и не дающих дополнительной информации.

Обобщенным параметром оптимизации Y называют параметр сформированный на основе группы частных параметров y₁, y₂,… y_m. Для его получения используют неравноценные по трудоемкости и эффективности приемы.

Линейная «свертка» параметров проводится с помощью весовых коэффициентов m_i, величина которых задается с учетом значимости вклада каждого частного параметра

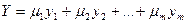. (18.1)

Если значения y₁, y₂,… y_m приведены к относительным единицам измерения, тогда m₁+m₂+…m_m=1. Если по каждому из частных параметров ввести норматив y^* , тогда коэффициенты m_i целесообразно задать с таким учетом, чтобы они давали наибольший вес параметру, для которого экспериментально достигнуто наихудшее приближение к нормативу. В этом случае оптимизация процесса по формуле (18.1) будет происходить преимущественно в направлении улучшения параметров, наиболее далеких от заданного норматива.

Ранжирование частных параметров осуществляется по номеру занимаемого места с введением обобщенного рангового параметра

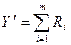, (18.2)

\или

. (18.3)

В случае одинаковой величины параметрам присваиваются дробные значения рангов, при которых сохраняется их общая сумма.

Функция желательности d позволяет нормировать частные значения параметров y_i и пересчитать их в значения желательности d­_i, из которых формируется обобщенная функция желательности

, (18.4)

выступающая в качестве параметра оптимизации.

Шкала желательности задается в пределах от 0 до 1 оценками «Очень хорошо» (1,00-0,80), «Хорошо» (0,80-0,63), «Удовлетворительно» (0,63-0,37), «Плохо» (0,37-0,20) и «Очень плохо» (0,20-0) (рис.18.1).

Определив, что такое «Хорошо» и что такое «Плохо» для частного параметра, графически преобразуют значения y_i в d_i (рис.18.1) с использованием нормирующей функции

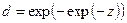, (18.5)

где z - кодированная шкала, пропорциональная натуральным значениям параметров.

Значения d_i (18.5) используют для расчета и поиска максимума D (18.4), аналогично рангам R_i при оптимизации параметра 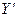(18.2) или 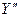(18.3).

Лекция №19