Выбор вида статистической модели
Приступая к построению статистической модели, экспериментатор обычно имеет начальные представления о том, как влияют изучаемые факторы на выходные параметры.
При выборе вида модели обычно отвечают на вопрос, допустимо ли представлять функцию отклика линейной или заведомо известно, что зависимости являются немонотонными или сильно нелинейными. В области, где функция отклика имеет экстремум, предположение о линейном характере модели скорее всего не будет подтверждено. Если в дальнейшем потребуется, могут быть проведены дополнительные опыты по уточнению вида модели. При этом результаты первой серии опытов не пропадают и используются в полной мере для построения нелинейной модели.
При планировании экспериментов исходный этап включает определение основного уровня факторов (X=0) и выбор интервалов варьирования DX с учетом области действия разрабатываемой модели, предполагаемого характера поверхности отклика и вероятной погрешности определения параметров Y, а также точности фиксирования принятых уровней факторов. Чем больше погрешность опытов и ниже точность поддержания факторов, тем шире должны быть приняты их интервалы варьирования.
Рассмотрим основные виды линейных и нелинейных статических моделей.
1. При разработке линейной модели ограничиваются обычно варьированием факторов на двух уровнях. Для проведения полного факторного эксперимента (ПФЭ) при k факторах необходимо осуществить N=2k опытов со всевозможными сочетаниями двух (x=-1 и x=+1) уровней факторов (табл.20.1)
Таблица 20.1
Матрица планирования ПФЭ 22
| № опыта | Факторы xi | |
| x1 | x2 | |
| + | + | |
| + | — | |
| — | + | |
| — | — |
Матрица планирования ПФЭ 23 получается повторением матрицы ПФЭ 22 для факторов x1 и x2 при x3=-1 и x3=+1 (табл.20.2).
Таблица 20.2
Матрица планирования ПФЭ 23
| № опыта | Факторы xi | ||
| x1 | x2 | x3 | |
| + | + | + | |
| + | — | + | |
| — | + | + | |
| — | — | + | |
| + | + | — | |
| + | — | — | |
| — | + | — | |
| — | — | — |
Аналогичным образом могут быть построены матрицы планирования с большим числом факторов, однако при этом число опытов быстро растет и при k³5 становится весьма значительным. При этом количество опытов (2k) намного превышает число неизвестных коэффициентов регрессии (k+1) линейной модели.
Для построения трех факторной модели необходимо определить четыре коэффициента (b0, b1, b2, b3), поэтому достаточно всего четырех опытов и можно воспользоваться дробным факторным экспериментом (ДФЭ) - половиной ПФЭ 23, называемой полурепликой 23-1 . Для этого надо выбрать из опытов, матрицы ПФЭ 23 (табл.20.2), такие, в которых бы факторы x1, x2, x3, равномерно принимали все возможные значения. Если воспользоваться генерирующим соотношением, x3=+x1x2 (или x3=-x1x2), то можно получить две антисимметричные экономные матрицы ДФЭ, одинаково пригодные для построения модели 23-1 (табл.20.3)
Таблица 20.3
Матрица планирования ДФЭ 23-1 (x3=-x1x2)
| № опыта | Факторы xi | ||
| x1 | x2 | x3 | |
| + | + | — | |
| + | — | + | |
| — | + | + | |
| — | — | — |
Аналогичным образом могут быть построены полуреплики, четверть реплики, и реплики более высокой дробности ПФЭ 2k , что дает существенную экономию количества опытов.
Например для k=6 ПФЭ требует проведения 26=64 опытов. Однако для определения 7 коэффициентов линейного уравнения регрессии задачу можно решать, проведя всего 8 опытов, т.е. осуществив ДФЭ 26-3 в котором реплика дробности 1/8. Рекомендуемыми генерирующими соотношениями при этом могут быть x4= x1x2x3, x5= x1x2, x6= x1x3 или др.
2. При построении нелинейной модели, учитывающей кроме линейных членов также некоторые взаимодействия (xixj), в матрицу вводят дополнительные столбцы, содержащие соответствующие произведения факторов (табл.20.4) и увеличивают число опытов.
Таблица 20.4
Матрица планирования ДФЭ 24-1 (x4= x1x2x3)
| № опыта | Факторы xi | Взаимодействующие факторы xi xj | ||||||
| x0 | x1 | x2 | x3 | x4 | x1 x2 | x2 x4 | x2 x3 | |
| + | + | + | + | + | + | + | + | |
| + | — | + | + | — | — | — | + | |
| + | + | — | + | — | — | + | — | |
| + | — | — | + | + | + | — | — | |
| + | + | + | — | — | + | — | — | |
| + | — | + | — | + | — | + | — | |
| + | + | — | — | + | — | — | + | |
| + | — | — | — | — | + | + | + | |
| + | ||||||||
| + | ||||||||
| + |
Так, планируя выявить эффекты взаимодействия факторов x1x2, x2x4, и x2x3 при k=4 можно воспользоваться восемью опытами, если для построения матрицы экспериментов воспользоваться генерирующим соотношением, например x4= x1x2x3 (табл.20.4). Это позволяет найти четыре коэффициента для линейных членов(b1, b2, b3, b4,), свободный член (b0) и три эффекта взаимодействия (b12, b24, b23).
Условия проведения опытов задают значения факторов в столбцах x1, x2, x3, x4. Столбец x0 заполнен знаками «+», а столбцы x1x2, x2x4, x2x3, , образованы как произведения соответствующих столбцов и применяются при последующем вычислении коэффициентов регрессии.
Матрицы планирования экспериментов (табл.20.1-20.4) формируются таким образом, чтобы выполнить обеспечивающие простоту вычисления и оптимальные оценки коэффициентов модели требования:
1. Нормировки - сумма квадратов элементов каждого столбца равна числу элементов N:
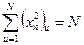 .
.
2. Симметрии - сумма элементов каждого столбца равна нулю:
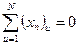 .
.
3. Ортогональности - сумма произведений элементов каждой пары столбцов равна нулю.
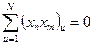 ;
;  .
.
При выполнении этих требований все коэффициенты регрессии определяются независимо друг от друга с одинаковой погрешностью по результатам всех N опытов.
Лекция №21
Ортогональное планирование экспериментов
Если поверхность отклика является существенно нелинейной, тогда в уравнение модели необходимо ввести квадратичные члены второго порядка. Для этого достраивают матрицу в соответствии с планами эксперимента второго порядка.
Расширенная матрица содержит:
— N1 опытов в точках ДФЭ - ядро плана, из которого определяются линейные члены и их взаимодействия;
— n0 опытов в центре плана, для оценки ошибки опытов;
— 2k дополнительных опытов в «звездных» точках, расположенных по координатным осям на расстоянии ±a.
Отсюда общее число опытов:
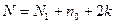
Число уровней варьирования каждого фактора (-a;-1;0;+1;+a) равно 5. Для облегчения вычислений и для того, чтобы параметры модели определялись независимо, план должен быть ортогональным. Это достигается введением вместо 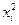 нового нормализованного фактора.
нового нормализованного фактора.
 ,
,
где u - номер опыта, 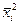 - среднее значение
- среднее значение 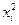 .
.
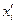 при числе факторов k=2,3,4,5 соответственно равняется 0,667;0,73;0,80;0,776. (при k=5 применяется полуреплика). Кроме того выбирается «звездное» плечо a по формуле.
при числе факторов k=2,3,4,5 соответственно равняется 0,667;0,73;0,80;0,776. (при k=5 применяется полуреплика). Кроме того выбирается «звездное» плечо a по формуле.
 .
.
В силу ортогональности планирования все параметры нормализованной модели второго порядка определяются независимо друг от друга:
 ;
;  , (i¹j);
, (i¹j);
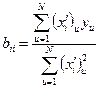 ;
; 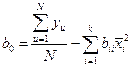 .
.
В числителях данных формул находятся суммы произведений значений отклика yu и значений нормализованного фактора в соответствующем столбце xiu, а в знаменателе - сумма квадратов значений нормализованных факторов из соответствующих столбцов.
Дисперсия оценок параметров модели находится по формулам:
 ;
; 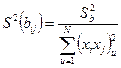 ;
;
 ;
; 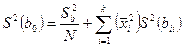 .
.
Недостатком центрального композиционного ортогонального планирования (ЦКОП) второго порядка является то, что параметры модели определяются с различной точностью, так как у них различны дисперсии. Поэтому информация о поверхности отклика, содержащаяся в модели, полученной после реализации ЦКОП второго порядка, различна в разных направлениях факторного пространства.
Лекция №22
Рототабельное планирование экспериментов
Существует другой способ центрального композиционного планирования второго порядка, позволяющий при помощи полученной модели описывать поверхность отклики с одинаковой точностью по всем направлениям, при этом остаточные дисперсии на одинаковых расстояниях от центра плана являются равными и наименьшими из возможных. Такое планирование получило название рототабельного. При центральном композиционном рототабельном планировании (ЦКРП) значение звездного плеча определяется о формуле:
 ,
,
где N1 - число опытов ядра плана
В зависимости от выбора числа опытов в центре плана обеспечивается либо так называемая униформность, либо ортогональность плана. В первом случае дисперсия предсказания сравнительно мало изменяется или совсем не изменяется в радиусе xn=±1 от центра плана. Для обеспечения униформности плана должно соблюдаться равенство
 ,
,
в котором l для числа факторов k=2,3,4,5,6,7 равно соответственно 0,7844; 0,8385; 0,8705; 0,8918; 0,9070; 0,9185.
Чтобы рототабельный план был ортогональным, число опытов в центре плана должно соответствовать равенству
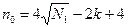 ,
,
полученному из предыдущего при l=1. Расчет по нему в некоторых случаях дает дробные значения n0, поэтому их приходится округлять до ближайшего целого числа, нарушая при этом условия униформности. Однако эти отклонения оказываются настолько незначительными, что ими можно пренебречь.
Для построения матриц центрального композиционного рототабельного униформ планирования (ЦКРУП) рассчитывается и используется ряд характеристик (табл.22.1)
Таблица 22.1
Характеристики ЦКРУП второго порядка
| Число факторов, k | Число опытов ядра, N1 | Число «звездных» точек, 2k | Число нулевых точек, n0 | «Звездное» плечо, a | Общее число опытов, N |
| 1,414 | |||||
| 1,682 | |||||
Матрицы рототабельного униформ-планирования не ортогональны, поэтому параметры модели рассчитываются более сложным способом, чем при ортогональном планировании:
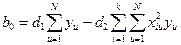 ;
;
 ;
;
 , (i¹j);
, (i¹j);

Дисперсии параметров модели
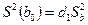 ;
;  ;
;
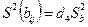 ;
;  .
.
Соответствующие условиям опытов значения di выбираются для конкретных случаев планирования эксперимента (табл.22.2)
Таблица 22.2
Значения di для вычисления параметров модели
| k | N | d1 | d2 | d3 | d4 | d5 | d6 | d7 |
| 0,2 | 0,1 | 0,1250 | 0,2500 | 0,1251 | 0,0187 | 0,1438 | ||
| 0,1663 | 0,0568 | 0,0732 | 0,1250 | 0,0625 | 0,0069 | 0,0695 | ||
| 0,1428 | 0,0357 | 0,0417 | 0,0625 | 0,0312 | 0,0037 | 0,0350 | ||
| 0,1591 | 0,0341 | 0,0417 | 0,0625 | 0,0312 | 0,0028 | 0,0341 |
Так как при планировании экспериментов несколько опытов проводятся параллельно при основном уровне факторов, то их результаты позволяют оценить дисперсию воспроизводимости
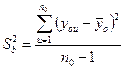 .
.
Проверка адекватности модели производится при помощи критерия Фишера. Дисперсия адекватности в данном случае определяется по формуле:
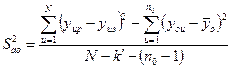 ,
,
где yup и yuэ – расчетные и экспериментальные значения;  - число статистически значимых параметров модели.
- число статистически значимых параметров модели.
При использовании рототабельных планов исключать из модели без пересчета остальных можно только незначимые оценки bi и bij . Исключение любого из незначимых параметров b0 и bii требует пересчета остальных в данной группе.
При реализации намеченных планированием экспериментов важно учитывать требования рандомизации опытов, т.е. проведения опытов в однородных условиях, с одинаковой погрешностью в случайном порядке. Рандомизация проводится для того, чтобы изменения свойств материалов, характеристик оборудования, средств оснащения, установок и измерительных приборов вследствие их износа и разрушения, смены персонала и т.д. не вызывали, искажающего влияния изучаемых факторов и временного «дрейфа» параметров. Поэтому рандомизируют опыты, проводя их в случайном порядке, в отличие от нумерации в матрице планирования.
Лекция №23
Дата добавления: 2015-11-06; просмотров: 1326;
