Проверка адекватности моделей

Адекватностью называют соответствие математической модели процесса экспериментальным данным. Проверка адекватности аналитической модели состоит в поиске ответа на вопрос о том, соответствует ли натурным данным полученные теоретические зависимости.

Для однозначного ответа на вопрос об адекватности детерминированной модели применительно к стохастическим переменным системы целесообразно воспользоваться процедурой корреляционного анализа, вычислив значения коэффициента линейной корреляции между переменными y и x:

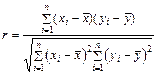(19.1)

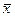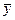где x_i и y_i - пара соответствующих значений x и y в каждой i-той опытной точке, и - средние значения x и y.

Адекватность модели обеспечивает статистически значимая линейная корреляция с уровнем значимости a (обычно берут a³0,95). Если r>r_кр(a,n), в котором критическое значение r_кр зависит от принятого уровня значимости a и числа опытных точек n, то модель адекватна.

Для программных моделей проверка адекватности является этапом более сложным, чем для теоретических моделей, так как коэффициент корреляции (19.1) может быть использован ограниченно лишь для тех стадий процесса, которые приближенно описываются полученными для упрощенных условий аналитическими моделями.

В общем случае проверка адекватности для программных моделей состоит в сопоставлении расчетных y_р и экспериментальных y_э значений, и оценке величины коэффициентов парной корреляции 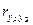по формуле (19.1) и коэффициента линейной регрессии:

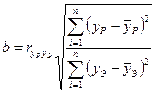(19.2)

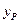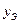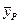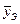где и - пары соответственных значений расчетных и экспериментальных данных; и - средние значения 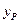и 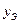по совокупности всех n сопоставляемых величин.

Когда r<r_кр, модель неадекватна, в связи с чем следует пересмотреть начальные этапы построения модели и внести в них необходимые корректировки.

Если r>r_кр, а b»1 (19.2), то можно сделать вывод об адекватности модели. Если при r>r_кр, b><1 можно говорить о принципиальной адекватности полученной модели на основе тесной зависимости между расчетными и экспериментальными данными, а также заключить о необходимости корректировки параметров модели, количественной мерой которой является отличие коэффициента регрессии b от 1.

Корректировка параметров модели является частным случаем более общей процедуры параметризации модели, т.е. подбора таких значений коэффициентов уравнений, входящих в математическую модель, при которых достигается наилучшее согласование модели и натуры.

Обычно используют наиболее доступные возможности оценки параметров модели, т.е. обращение к табличным данным или теоретическому расчету, а также их независимое экспериментальное определение по другим методикам. Если это невозможно, тогда для установления величины какого-либо неопределенного параметра k полученной программной модели проводят серию вычислений, каждый раз варьируя значение этого параметра в пределах предполагаемого интервала его изменения. При этом рассчитывают значения одного или нескольких индикаторов, т.е. таких выходных характеристик процесса y^*, которые наиболее чувствительны к параметру k и поддаются экспериментальному определению ( 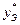), получив расчетную зависимость y^*(k), нетрудно установить искомое значение параметра k₀, при котором .

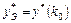Таким образом, модели основных физико-технических процессов в рабочей зоне технологической системы базирующиеся на системах уравнений баланса и краевых условиях или использующие структурные представления для идеальных и неидеальных технологических потоков, а также их комбинации позволяют создавать адекватные математические модели детерминированных систем как с сосредоточенными, так и с распределенными параметрами и находить методы и алгоритмы решения технологических задач.

Лекция №20

МАТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ В ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССАХ