Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 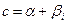 и
и 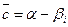 корни
корни 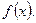 Тогда
Тогда 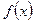 делится на
делится на 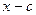 и
и 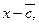 но так как у
но так как у 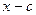 и
и 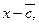 нет общих делителей, то
нет общих делителей, то 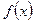 делится на прозведение
делится на прозведение 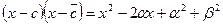 .
.
Утверждение 2. Многочлен с действительными коэффициентами степени 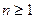 всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь 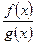 где
где 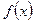 и
и 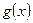 ‑ многочлены с действительными коэффициентами, причем многочлен
‑ многочлены с действительными коэффициентами, причем многочлен 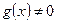 . Рациональная дробь
. Рациональная дробь 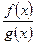 называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде
называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде 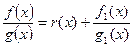 , где
, где 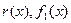 и
и 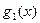 – некоторые многочлены, а
– некоторые многочлены, а 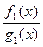 – правильная рациональная дробь.
– правильная рациональная дробь.
Лемма 1. Если – правильная рациональная дробь, а число является вещественным корнем кратности многочлена , т.е. и , то существует вещественное число и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если – правильная рациональная дробь, а число ( и – вещественные, ) является корнем кратности многочлена , т.е. и , и если , то существуют вещественные числа и и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.
Рациональные дроби вида 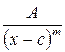 ,
, 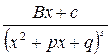 ,
, 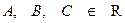 ,
, 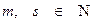 ,
, 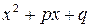 ‑ трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
‑ трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов. Он состоит в следующем:
· Для данной дроби 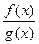 пишется разложение, в котором коэффициенты
пишется разложение, в котором коэффициенты 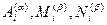 считаются неизвестными
считаются неизвестными 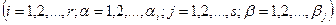 ;
;
· После этого обе части равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты.
При этом если степень многочлена 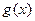 равна
равна  , то в числителе после приведения к общему знаменателю получается многочлен степени
, то в числителе после приведения к общему знаменателю получается многочлен степени 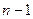 , т.е. многочлен с
, т.е. многочлен с  коэффициентами.
коэффициентами.
Число неизвестных 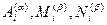 также равняется
также равняется  :
: 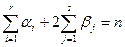 .
.
Таким образом, получается система  уравнений с
уравнений с  неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
Контрольные вопросы к лекции №11
1. Понятие многочлена.
2. Условие равенства многочленов.
3. Сложение и умножение многочленов.
4. Теорема о делении с остатком.
5. Понятие корня многочлена.
6. Понятие кратности корня многочлена
7. Теорема Безу.
8. Схема Горнера.
9. Соотношение степени многочлена и числа его корней.
10. Понятие правильной рациональной дроби.
11. Разложение правильной рациональной дроби на простейшие.
12. Метод неопределенных коэффициентов.
Дата добавления: 2015-10-09; просмотров: 1157;
