Теорема Безу
Число 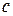 является корнем многочлена
является корнем многочлена 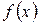 тогда и только тогда, когда
тогда и только тогда, когда 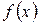 делится на
делится на 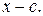
Пусть 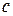 ‑ корень многочлена
‑ корень многочлена 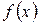 , т.е.
, т.е. 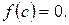 Разделим
Разделим 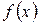 на
на 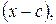
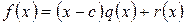 ,где степень
,где степень 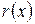 меньше степени
меньше степени 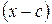 , которая равна
, которая равна 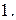 Значит, степень
Значит, степень 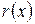 равна
равна 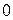 , т.е.
, т.е.  . Значит,
. Значит,  ,
, 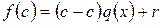 . Так как
. Так как 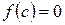 , то из последнего равенства следует, что
, то из последнего равенства следует, что 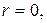 т.е.
т.е.  .
.
Обратно, пусть 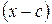 делит
делит 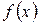 , т.е.
, т.е.  . Тогда
. Тогда 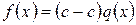 .
.
Дата добавления: 2015-10-09; просмотров: 643;
