Теорема. Матрица является ортогональной тогда и только тогда, когда .
В соответствии с этой теоремой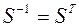 
, и преобразование 
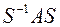эквивалентно преобразованию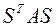 
При определении характеристических чисел матрицы было введено новое понятие характеристического многочлена. Подробный анализ понятия многочлена приводится в следующем разделе.
Контрольные вопросы к лекции №10
1. Переход к новому базису и понятие матрицы перехода.
2. Понятие линейного оператора.
3. Собственные значения и собственные вектора матрицы.
4. Операция диагонализации матрицы и понятие ортогональной матрицы.
Дата добавления: 2015-10-09; просмотров: 660;