Теорема. Если и – два различных собственных значения симметрической матрицы , то соответствующие им собственные векторы и удовлетворяют соотношению , т.е. они ортогональны.

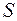Таким образом, собственные значения симметрической матрицы различны, а, значит, если пронормировать соответствующие им собственные векторы, то система собственных векторов матрицы станет ортонормированной, а матрица , столбцами которой будут эти векторы, станет ортогональной.

Ортогональной называется вещественная квадратная матрица, у которой соответствующая ей система векторов-столбцов является ортонормированной системой евклидова пространства.