Переход к новому базису. Пусть в пространстве R имеются два базиса: старый и новый
Пусть в пространстве R имеются два базиса: старый 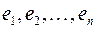 и новый
и новый  . Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
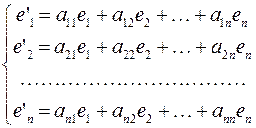
Полученная система означает, что переход от старого базиса 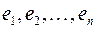 к новому
к новому 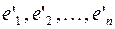 задается матрицей перехода:
задается матрицей перехода:
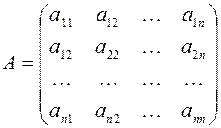 ,
,
причем, коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица  — неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса
— неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 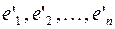 к старому базису
к старому базису 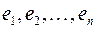 осуществляется с помощью обратной матрицы
осуществляется с помощью обратной матрицы  .
.
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 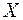 имеет координаты
имеет координаты 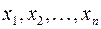 относительно старого базиса и координаты
относительно старого базиса и координаты  относительно нового базиса, т.е.:
относительно нового базиса, т.е.:
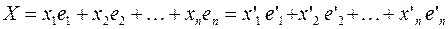
Подставив значения 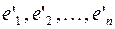 из системы в левую часть этого равенства, получим после преобразований:
из системы в левую часть этого равенства, получим после преобразований:
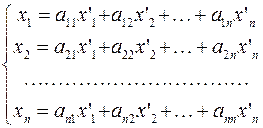
т.е. в матричной форме:  или
или 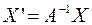
Дата добавления: 2015-10-09; просмотров: 792;
