Теорема 2. Матрица имеет обратную матрицу тогда и только тогда, когда .
Пусть 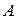 имеет обратную матрицу. Тогда
имеет обратную матрицу. Тогда  и, применяя теорему об умножении определителей, получаем
и, применяя теорему об умножении определителей, получаем 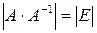 или
или  . Следовательно,
. Следовательно,  .
.
Пусть  . Укажем явное выражение матрицы
. Укажем явное выражение матрицы 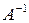 через элементы матрицы
через элементы матрицы 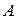 , а именно: если
, а именно: если  , то:
, то:
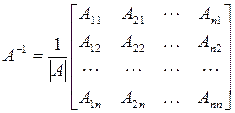 , ,
| (9.5) |
здесь 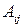 ‑ алгебраическое дополнение к элементу
‑ алгебраическое дополнение к элементу 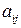 . Матрица (9.5) получается из матрицы
. Матрица (9.5) получается из матрицы 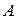 следующим образом. Сначала вместо каждого элемента
следующим образом. Сначала вместо каждого элемента 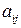 пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную
пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную  .
.
Непосредственное умножение 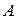 на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к
на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к 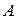 .
.
Пример 12. Найти обратную матрицу к матрице  .
.
Так как 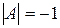 , то
, то 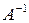 существует. Вычислим алгебраические дополнения элементов матрицы
существует. Вычислим алгебраические дополнения элементов матрицы 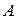 :
:
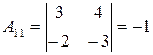 , ,
|  , ,
|
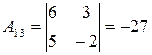 , ,
|  , ,
|
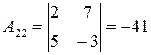 , ,
| 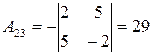 , ,
|
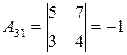 , ,
|  , ,
|
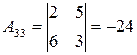 . .
|
Матрицу 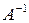 находим в два приема, согласно формуле (9.5). Сначала запишем матрицу
находим в два приема, согласно формуле (9.5). Сначала запишем матрицу 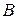 , состоящую из алгебраических дополнений элементов
, состоящую из алгебраических дополнений элементов 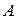 .
.  Затем матрица
Затем матрица 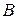 транспонируется и умножается на число обратное
транспонируется и умножается на число обратное  , в данном случае – на (-1). Окончательно получаем:
, в данном случае – на (-1). Окончательно получаем:
 .
.
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если 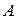 и
и 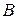 ‑ невырожденные матрицы одинакового порядка, то:
‑ невырожденные матрицы одинакового порядка, то:
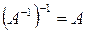 ,
,
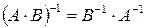 ,
,
 ,
,
 .
.
Контрольные вопросы к лекции №9
1. Понятие матрицы.
2. Виды матриц.
3. Понятие транспонирования матриц.
4. Операции сложения и вычитания матриц.
5. Операции умножения и возведения в степень матриц.
6. Понятие определителя.
7. Определитель  - го порядка.
- го порядка.
8. Правила нахождения определителей 2 и 3 порядка.
9. Свойства определителей.
10. Правила нахождения определителей  - го порядка.
- го порядка.
11. Понятие обратной матрицы.
12. Схема нахождения обратной матрицы.
13. Понятие ранга матрицы.
Дата добавления: 2015-10-09; просмотров: 669;
