Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

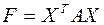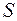Пусть дана квадратичная форма , Поскольку – симметрическая матрица, для нее существует диагонализирующая ортогональная матрица , такая что:

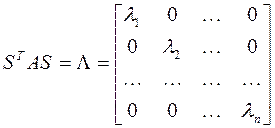
где – собственные значения матрицы .

Применим к квадратичной форме линейное преобразовани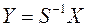е , где 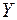– матрица-столбец новых переменных 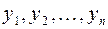; 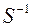– матрица, обратная к .

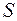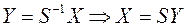
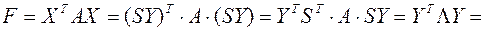
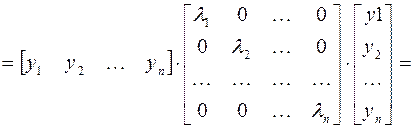
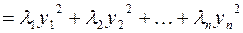
Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Наиболее удобным для исследования является канонический вид, в котором коэффициенты при новых переменных равны +1
или –1, т.е. квадратичная форма имеет вид:

.

Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу 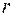квадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема. Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

Базис 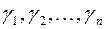пространства 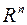называется каноническим базисом квадратичной формы 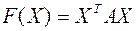, если в этом базисе квадратичная форма имеет канонический вид, т.е. 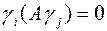при .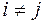

Если 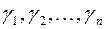– канонический базис 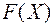, то выражение:

,

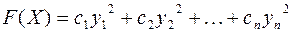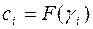
называется каноническим видом 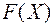в базис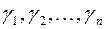е , где 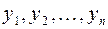– новый набор неизвестных.

Теорема. Если 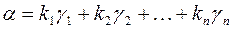– разложение вектора 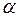по каноническому базису 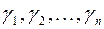квадратичной формы 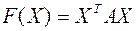, то значение 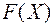на векторе 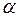вычисляется по формуле , .

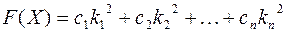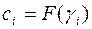Доказательство:

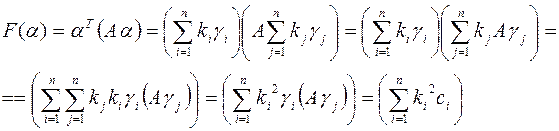
Эта теорема утверждает, что если известны канонический базис 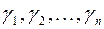квадратичной формы 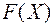и ее канонический вид 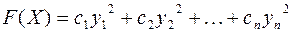в этом базисе, то для вычисления значения 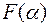квадратичной формы 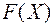на векторе 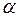достаточно:

1. разложить вектор 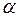по каноническому базису :

;

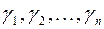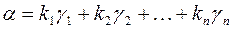2. коэффициенты разложения 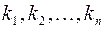подставить вместо неизвестных 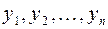в канонический вид квадратичной формы:

.

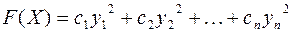Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы и канонический базис Якоби.