Положительно и отрицательно определенные квадратичные формы
Квадратичная форма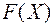 
называется положительно определенной, если значение 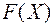на каждом ненулевом значении 
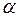больше нуля, т.е.:
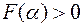, если 
, 
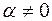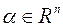
Если же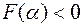 
на каждом 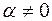, то квадратичная форма называется отрицательно определенной.
Теорема. Дана квадратичная форма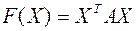 
, 
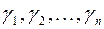– ее канонический базис, а выражение 
, 
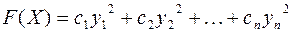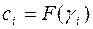канонический вид 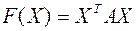в базисе 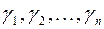. Тогда справедливы следующие утверждения:
Дата добавления: 2015-10-09; просмотров: 618;