Лемма. Если какой-нибудь угловой минор матрицы равен нулю, то найдется такой ненулевой вектор , что .

Теорема (Критерий Сильвестра). Справедливы следующие утверждения:

Квадратичная форма положительно определена тогда и только тогда, когда главные миноры матрицы положительны.

Квадратичная форма отрицательно определена тогда и только тогда, когда главные миноры матрицы четного порядка положительны, а главные миноры матрицы нечетного порядка отрицательны.

Доказательство: Докажем первое утверждение.

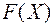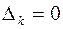Необходимость. Дано, что положительно определена. Покажем, что все угловые миноры матрицы отличны от нуля. Допустим обратное, и пусть . Тогда согласно Лемме найдется такой ненулевой вектор , что . Однако это противоречит положительной определенности квадратичной формы.

Итак, матрица удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби 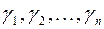, которая является каноническим базисом 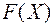, причем выражение 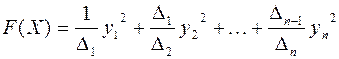– ее канонический вид в базисе 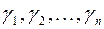. Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что 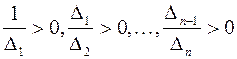, и значит, что .

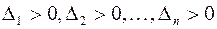Достаточность. Если 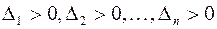, то угловые миноры матрицы отличны от нуля, и можно построить канонический базис квадратичной формы 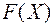, в котором 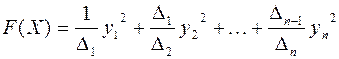– канонический вид квадратичной формы 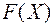. Поскольку 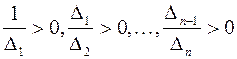, то 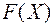положительно определена.

Аналогично доказывается второе утверждение теоремы.