Лекция 13. Системы линейных уравнений
Основные понятия:
система линейных уравнений; решение системы линейных уравнений; совместная система линейных уравнений; определенная система линейных уравнений; эквивалентные системы линейных уравнений; матрица системы; расширенная матрица системы линейных уравнений; теорема Кронекера-Капелли; правило Крамера; метод Гаусса; однородная система линейных уравнений; разрешенная переменная; набор разрешенных переменных; свободные переменные.
Основные понятия
Для исследования процессов функционирования экономики, при построении математических моделей конкретных задач, возникающих перед менеджером в процессе его деятельности, в ряде случаев используются системы линейных уравнений. Так, например, при межотраслевом анализе – изменение объема выпуска отрасли при фиксированном коэффициенте прямых затрат в случае изменения спроса необходимо искать путем решения системы линейных уравнений, которая является моделью изучаемого процесса.
Нахождение решений системы линейных уравнений может быть осуществлено различными методами. Выбор метода зависит от рассматриваемой задачи и соответствующей математической модели.
В ряде случаев необходимо лишь знать – существует ли решение рассматриваемой системы.
Цель данного раздела – исследовать совместность системы линейных уравнений и дать некоторые методы их решения. Эти методы позволяют найти точное решение системы. Кроме этого, существуют методы, позволяющие находить приближенные решения, например, метод Якоби, метод Гаусса-Зейделя, метод пошагового агрегирования. В этом разделе они не рассматриваются.
Рассмотрим совокупность уравнений:
 , ,
| (13.1) |
где 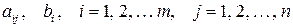 ‑ действительные числа, а
‑ действительные числа, а  ‑ неизвестные. Эту совокупность называют системой линейных уравнений с
‑ неизвестные. Эту совокупность называют системой линейных уравнений с 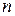 неизвестными, числа
неизвестными, числа 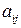 ‑ коэффициенты системы (1),
‑ коэффициенты системы (1),  ‑ свободные члены. Упорядоченный набор
‑ свободные члены. Упорядоченный набор 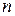 действительных чисел
действительных чисел  называется решением системы (13.1), если после подстановки в каждое из уравнений (13.1) вместо
называется решением системы (13.1), если после подстановки в каждое из уравнений (13.1) вместо  чисел
чисел 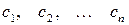 , это уравнение превращается в тождество.
, это уравнение превращается в тождество.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения.
Система называется определенной, если она имеет единственное решение, и неопределенной, если у нее есть, по крайней мере, два различных решения.
Две системы с  неизвестными называются эквивалентными, если множества их решений совпадают.
неизвестными называются эквивалентными, если множества их решений совпадают.
Матрица 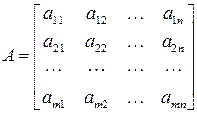 , составленная из коэффициентов системы (13.1), называется матрицей системы.
, составленная из коэффициентов системы (13.1), называется матрицей системы.
Обозначив через  , систему (13.1) можно записать в виде матричного уравнения:
, систему (13.1) можно записать в виде матричного уравнения:
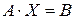
| (13.2) |
Матрица 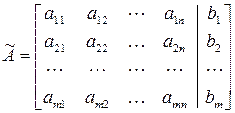 , полученная приписыванием к матрице
, полученная приписыванием к матрице 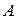 справа столбца свободных членов системы (13.1), называется расширенной матрицей системы (13.1).
справа столбца свободных членов системы (13.1), называется расширенной матрицей системы (13.1).
При исследовании системы (13.1) ищут ответ на следующие три вопроса:
1. когда система совместна;
2. если система совместна, то определена ли она;
3. как отыскать ее решения.
Дата добавления: 2015-10-09; просмотров: 682;
