Квадратичная форма отрицательно определена тогда и только тогда, когда все собственные значения матрицы отрицательны.

Доказательство:

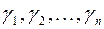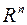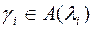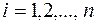Докажем первое утверждение. Рассмотрим ортонормированный базис пространства , состоящий из собственных векторов симметрической матрицы , и пусть , . Тогда 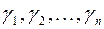– канонический базис квадратичной формы 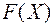, а выражение 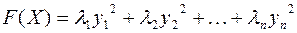– ее канонический вид в базисе 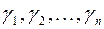. Теперь первое утверждение этой теоремы вытекает из первого предложения предыдущей теоремы.

Второе предложение доказывается аналогично.