Канонический базис квадратичной формы

Принято считать, что квадратичная форма 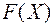имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. 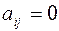при . При 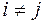этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами 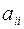, т.е.:

.

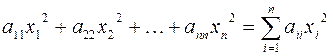В этом случае матрица квадратичной формы имеет диагональный вид:

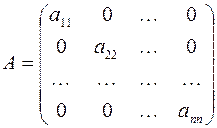
Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.