Наступні наближення одержуються за схемою

,

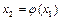, (3.12)

…………,

.

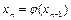Якщо послідовність 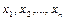має межу , то є коренем рівняння (3.11). Насправді, припускаючи, що неперервна функція, одержимо

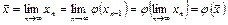, (3.13)

тобто

. (3.14)

Отже, є коренем нашого рівняння. Тому одне з значень 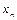з досить ве­ликим номером можна прийняти за наближене значення кореня. Але може виявитись, що послідовність 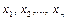не має межі, і тоді метод ітерацій не веде до мети.

Становить великий інтерес виявлення умов, при яких ітераційний процес сходиться. Є наступна теорема.

Т е о р е м а. Нехай інтервал 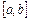є інтервалом ізоляції кореня рівняння 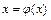і в усіх точках цього інтервалу похідна задовільняє нерівності .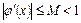

Якщо при цьому виконується умова , то ітераційний процес сходиться, причому за нульове наближення 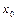можна брати довільну точку інтервалу .

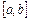Тут 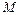– найбільше значення першої похідної.

Згідно з теоремою, для сходимості ітераційного процесу достатньо, щоб нерівнісь додержувалась на інтервалі, який роз­глядається. Тоді умова наближення кореня виглядає наступним чином

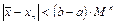. (3.15)

Формули прямокутників і трапецій. Формули для наближеного визначення означених інтегралів, які часто називаються квадратурними формулами, вживаються дуже часто. Справа в тому, що для великого числа елементарних функцій первісні вже не виражаються через еле­ментарні функції, в результаті чого не можна обчислити означений ін­теграл за допомогою формули Ньютона-Лейбніца. Зустрічаються такі випадки, коли наближене інтегрування проводять для інтегралів, що можуть бути знайдені в кінцевому виді, але в цьому випадку їх вираз є досить складним. Особливо важливі формули наближеного інтегру­вання при розв'язуванні задач, які містять функції, задані таблично.

Найбільш простими формулами для чисельного інтегрування є формули прямокутників і трапецій. Вивід їх базується на використанні геометричного змісту означеного інтеграла, що є, як відомо, площею криволінійної трапеції.

Формула прямокутників, власне, є не що інше, як інтегральна сума, складена з врахуванням деяких додаткових припущень.

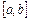Нехай потрібно обчислити інтеграл . Розіб'ємо ділянку ін­тегрування на 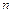рівних частин і помістимо точки, значення функції в котрих входять в інтегральну суму, в лівих кінцях одержаних ділянок. Якщо рахувати, що 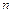досить велике, тобто довжина ділянки розбиття досить мала, то інтегральна сума повинна вже мало відрізня­тись від величини інтеграла. Таким чином одержуємо наближену рів­ність

, (3.16)

яка і є формулою прямокутників. Тут, як і в подальшому, через 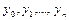позначені значення функції в точках ділення .

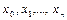Аналогічну формулу прямокутників одержимо і в тому випадку, коли для інтегральної суми брати значення функції не в лівих, а в пра­вих кінцях ділянок. Тоді формула має вид

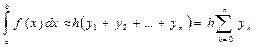. (3.17)

Для функції, монотонної на відрізку інтегрування, будь-яка інтег­ральна сума, а отже, і означений інтеграл знаходяться між наближеними значеннями, вказаними у правих частинах формул (3.8) і (3.9). Геомет­ричну ілюстрацію цього факту можна бачити на рисунку 3.2.

Це наводить на думку приймати в якості наближеного значення інтеграла математичне очікування наближень, одержаних за формулами (3.8) і (3.9).

Відзначимо, що нема сенсу обчислювати попередньо ці значення, так як можна відразу скористатись готовою формулою. Дійсно, взявши середнє арифметичне правих частин формул (3.8.) і (3.9.) одержимо

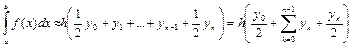. (3.18)

Це і є формула трапецій.

Рисунок 3.2 – Геометричний зміст методу прямокутників.

Формулу трапецій (3.18) можна легко одержати безпосередньо, вихо­дячи з її геометричного змісту (рисунок 3.3.). Розіб'ємо відрізок інтегрування на 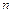рівних частин точками , проведемо ор­динати в усіх точках ділення і замінимо кожну з одержаних криволіній­них трапецій прямолінійною. Сторона кожної з цих трапецій є дві сусі­дні ординати, ділянка осі , довжина якої 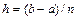, і хорда кривої. Площа самої лівої трапеції рівна . Аналогічно для трапеції, що розташована над ділянкою , знаходимо

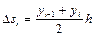. (3.19)

Сумування виразу (3.11) по всім 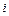від 1 до 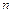і веде до формули (3.10), так як всі ординати, крім крайніх, використовуються у виразах виду (3.11) двічі.

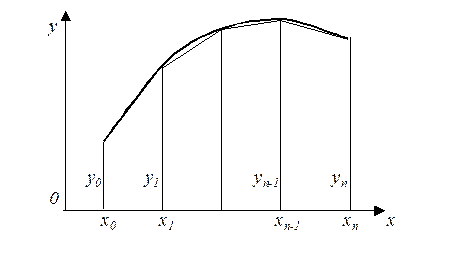Рисунок 3.3 – Геометричний зміст методу трапецій.

Формула Сімпсона. Більш точною, ніж розглянуті попередні, є формула Сімпсона. Для досягнення тієї ж точності в ній можна брати менше число ділянок розбиття і відповідно більший крок , тобто при тому ж об'ємі обчислень, вона дає меншу абсолютну і відносну по­хибки.

Формулу Сімпсона можна одержати за допомогою того ж при­йому, що й попередні. Розіб'ємо ділянку 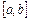на парне число час­тин точками , позначимо ординати в точках і розглянемо пару сусідніх ділянок, наприклад, з лівим кінцем в точці 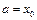(рисунок 3.4).

Рисунок 3.4 – Геометричний зміст методу Сімпсона.

Проведемо через три точки кривої з координатами 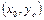, , 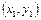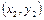параболу з віссю, паралельною осі 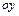. Її рівняння буде

, (3.20)

причому коефіцієнти А, В, С залишаються поки що невідомими.

Замінивши площу заданої криволінійної трапеції на ділянці 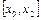площею криволінійної трапеції, яка обмежена параболою (3.20), при­йдемо до наближеної рівності

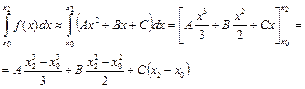. (3.21)

Виносячи за дужки спільний множник 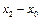і привівши до спільного знаменника, одержимо

. (3.22)

Невідомі коефіцієнти А, В, С в рівнянні (3.20) і формулі (3.22) знаходя­ться з умови, що при значеннях 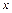, рівних , функція 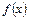приймає значення 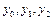. Відзначивши, що 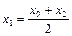, запишемо ці умови в ви­гляді

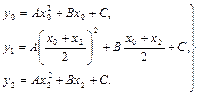. (3.23)

Помноживши другу рівність (3.23) на чотири і додавши після цього всі три рівності (3.23), знаходимо

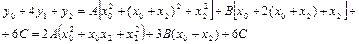, (3.24)

що співпадає з квадратними дужками в правій частині рівності (3.13).

Підставивши (3.15) в праву частину рівності (3.13) і відзначивши, що 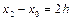, де , прийдемо до наближеної рівності

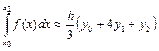. (3.25)

Ясно, що для кожної наступної пари ділянок одержимо таку ж формулу

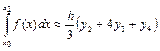. (3.26)

Сумуючи рівності виду (3.16) і (3.17) по всіх ділянках, одержимо фор­мулу

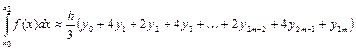. (3.27)

Формула (3.27) і є потрібна нам формула Сімпсона. Враховуючи геометричний зміст формули, її ще називають також формулою парабол. В ній всі ординати з непарними номерами множаться на чотири, а всі ординати з парними номерами (крім крайніх) – на два. Крайні ординати входять в формулу з коефіцієнтами рівними одиниці.

Метод Ейлера і його уточнення. Лише невелике число типів рів­нянь першого порядку допускає інтегрування в квадратурах, тобто зве­дення до звичайної операції інтегрування. Ще рідше вдається одержати розв'язок в елементарних функціях. Тим більше значення мають чис­ленні методи розв'язку диференційних рівнянь, які дозволяють вручну або за допомогою обчислювальної машини одержати таблицю значень функції в потрібних точках.

Розглянемо диференційне рівняння першого порядку, розв'язане відносно похідної,

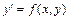. (3.28)

Загальним розв'язком такого рівняння є родина функцій 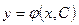, що залежить від довільної постійної. Щоб мати можливість обчислити зна­чення функції-розв'язку в деякій точці х, необхідно виділити з цієї ро­дини частковий розв'язок. Це робиться за допомогою завдання початко­вої умови виду

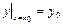. (3.29)

Знаходження розв'язку, який задовольняє такій умові, називають задачею Коші. В подальшому, говорячи про розв'язок диференційного рівняння першого порядку, завжди будемо мати на увазі рівняння виду (3.19) з початковою умовою (3.20).

Отже, задача численного розв'язку диференційного рівняння пер­шого порядку ставиться наступним чином: необхідно побудувати таб­лицю значень функції 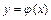, яка задовольняє рівнянню (3.19) і почат­ковій умові (3.20) на відрізку 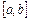з деяким кроком 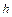(звичайно можна рахувати, що 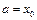, тобто початкова умова задана в лівому кінці зада­ного відрізку).

Найпростішим з численних методів інтегрування диференційних рівнянь є метод Ейлера. Звичайно він застосовується лише для наближених розрахунків, але ідеї покладені в його основує вихідними для широкого класу чисельних методів. Метод Ейлера заснований на заміні шуканої функції многочленом першого степеня, тобто на лінійній ін­терполяції. Проте, вірніше говорити про лінійну екстраполяцію, так як мова йде про знаходження значень функції в сусідніх вузлах, а не між вузлами.

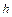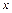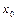Виберемо крок настільки малим, щоб для всіх між і 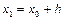значення функції мало відрізнялось від лінійної функції. Тоді на вказа­ному інтервалі

, (3.30)

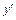де є значення похідної в точці 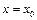. Таким чином, крива заміняється на цій ділянці відрізком прямої (дотичної до кривої на по­чатку ділянки). Для точки 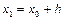одержимо

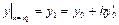. (3.31)

Також точно для можливо записати

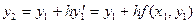. (3.32)

Продовжуючи таким чином будувати подальші значення функції, впев­нимось, що метод Ейлера можна подати в вигляді послідовного застосу­вання формул

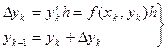. (3.33)

Геометричний зміст формули Ейлера зрозумілий з рисунку 3.5.

Інтегральна крива заміняється тут ламаною, ланки якої мають одну постійну проекцію 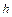. Перша ланка дотикається шуканої інтегральної кривої в точці .

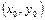Формули (3.21) можна одержати і з інших міркувань. З (3.19) ви­пливає

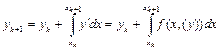. (3.34)

Вважаючи під інтегралом функцію 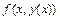рівною постійному зна­ченню у лівому кінці інтервалу інтегрування 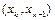, одер­жимо, що інтеграл рівний 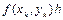, так що формула (3.22) перетвори­ться в (3.21).

Уточнений метод Ейлера при практично тому ж об'ємі обчислювальної роботи дає похибку порядку , замість 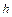в звичайному методі Ейлера, що досягається за допомогою досить простого прийому.

Рисунок 3.4 – Геометричний зміст формули Ейлера.

Повернемося до формули (3.22) при одержанні звідси формули (3.21) за методом Ейлера ми вважали підінтегральну функцію 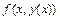постійною, рівною її значенню на лівому кінці ділянки. Більш точне значення одержиться, якщо вважати 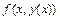рівною зна­ченню у центрі ділянки. Так як значення похідної між точками 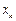і не обчислюється, то візьмемо подвійну ділянку 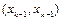, замінивши формулу (3.22) наступною

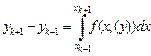. (3.35)

Центром інтервалу 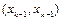є точка . Тому, замінивши в фор­мулі (3.23) під інтегралом функцію 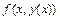її значенням в точці 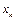, рі­вним 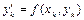, прийдемо до формули

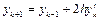. (3.36)

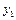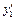Ця формула і виражає уточнений метод Ейлера. Проте вона може застосовуватись лише при , а значення одержати за нею немож­ливо. Отже не можна виконувати і подальших обчислень, так як для знаходження потрібно мати , для чого, в свою чергу, треба мати значення 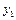. Значення 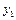можна знайти за допомогою звичайного методу Ейлера. Більш точні результати можна одержати, якщо спочатку знайти 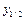у точці 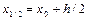за формулою (3.21), а потім шукати 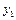за форму­лою (3.24) з кроком 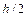. Інакше кажучи, рекомендується наступна по­слідовність дій:

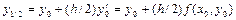, (3.37)

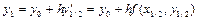, (3.38)

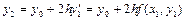. (3.39)

Після цього подальші обчислення йдуть вже за формулою (3.24) без змін.

Метод Рунге – Кутта. Метод Рунге – Кутта дуже часто використовує­ться для знаходження значень функцій в декількох початкових точках, завдяки тій особливості, що він зовсім не використовує попередньої інформації. Кожний крок в методі Рунге – Кутта робиться неначе знову, і для обчислення значень в точці використовується лише її значення у точці .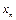

Розрахунком за таку малу інформативність метода є його трудомісткість. Для одержання наступного значення функції потрібно декілька разів обчислювати значення похідної 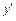, тобто звертатись до правої частини диференційного рівняння. Якщо ця права частина дуже громіз­дка, то трудомісткість буде в декілька разів переважати відповідну тру­домісткість методу Ейлера.

Існує декілька методів Рунге – Кутта різних порядків. Найбільш поширеним є метод четвертого порядку.

Дано диференційне рівняння першого порядку 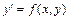і пере­дбачається відомим значення 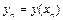. Не важливо, чи є 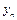заданим по­чатковим значенням, чи воно, в свою чергу одержане в результаті обчи­слень. Для одержання значення функції 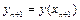за методом Рунге – Кутта виконується наступна послідовність операцій:

(3.40)

після цього приріст функції знаходиться за формулою

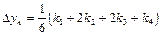, (3.41)

а

. (3.42)

Геометричний зміст цього методу легко прослідкувати за послідо­вністю формул (3.25), з яких видно, що кожний крок розрахунку являє собою, по суті, крок за методом Ейлера.