ЧИСЕЛЬНИЙ РОЗВ'ЯЗОК АЛГЕБРАЇЧНИХ І ТРАНСЦЕНДЕНТНИХ РІВНЯНЬ, ЧИСЕЛЬНЕ ІНТЕГРУВАННЯ
Як відомо, далеко не будь-яке рівняння може бути розв'язане точно. В першу чергу це відноситься до більшості трансцендентних рівнянь, тобто рівнянь, в яких невідома  знаходиться під знаком трансцендентної функції. Доведено також, що не можна побудувати формулу, за якою можна було б розв'язувати довільне алгебраїчне рівняння степеня вище четвертого. Доведення цього факту пов'язаний з іменами математиків Абеля (1802-1829) і Галуа (1811-1832).
знаходиться під знаком трансцендентної функції. Доведено також, що не можна побудувати формулу, за якою можна було б розв'язувати довільне алгебраїчне рівняння степеня вище четвертого. Доведення цього факту пов'язаний з іменами математиків Абеля (1802-1829) і Галуа (1811-1832).
Проте точний розв'язок рівняння не завжди необхідний. Задачу пошуку коренів рівняння можна рахувати практично розв'язаною, якщо ми зможемо визначити корені з відповідним степенем точності.
Більшість наближених методів розв'язку рівнянь є, по суті, способами уточнення коренів, тобто для їх застосування необхідно знати приблизне значення кореня. Для цієї мети служать графічні методи.
Нехай рівняння, яке розглядається має вид
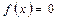 . (3.1)
. (3.1)
Побудуємо у декартовій системі координат схематичний графік функції 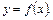 Абсциси точок перетину побудованої кривої з віссю
Абсциси точок перетину побудованої кривої з віссю  дадуть нам дійсні значення коренів рівняння (3.1).
дадуть нам дійсні значення коренів рівняння (3.1).
Після того, як схематичний графік побудовано і приблизно визначені ділянки осі абсцис, в яких будуть лежати корені функції, проводимо уточнення значень коренів. Для цього переходимо до аналітичних способів уточнення значень коренів. Відразу зауважимо: усі ці способи передбачають, що нам відомий інтервал 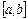 , в якому лежить корінь, що уточнюється. Вибір цього інтервалу проводиться на основі відомої властивості неперервний функцій: якщо функція
, в якому лежить корінь, що уточнюється. Вибір цього інтервалу проводиться на основі відомої властивості неперервний функцій: якщо функція 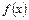 неперервна на замкнутому інтервалі
неперервна на замкнутому інтервалі 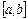 і на його кінцях має різні знаки, тобто
і на його кінцях має різні знаки, тобто 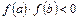 , то між точками
, то між точками 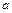 і
і 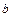 є хоча б один корінь рівняння
є хоча б один корінь рівняння 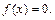
Нехай інтервал 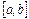 настільки малий, що в ньому лежить тільки один корінь нашого рівняння. Тоді говорять, що інтервал
настільки малий, що в ньому лежить тільки один корінь нашого рівняння. Тоді говорять, що інтервал 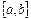 є інтервалом ізоляції кореня.
є інтервалом ізоляції кореня.
Звуження інтервалу ізоляції можна проводити найпростішим чином. Вибираємо будь-яку точку 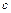 , яка лежить всередині інтервалу (звичайно за точку
, яка лежить всередині інтервалу (звичайно за точку 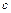 приймають середину інтервалу, що розглядається, або близьку до неї точку, в якій зручніше обчислювати значення функції) і обчислюємо значення
приймають середину інтервалу, що розглядається, або близьку до неї точку, в якій зручніше обчислювати значення функції) і обчислюємо значення 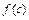 .
.
В якості нового інтервалу ізоляції приймаємо ту з двох половин інтервалу 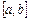 , на кінцях якої функція має різні знаки.
, на кінцях якої функція має різні знаки.
Таким шляхом можна як завгодно звузити ділянку, на якій знаходиться корінь, тобто одержати наближене значення кореня з будь-яким степенем точності. При цьому ми одержуємо оцінку точності наближеного розв'язку (корінь знаходиться між кінцями чергової дільниці). Але, незважаючи на принципову простоту, таке послідовне звуження дільниці на практиці не завжди проводиться, бо часто вимагає великої кількості обчислень і застосування ЕОМ.
При застосуванні інших способів уточнення кореня, будемо вимагати, щоб на відрізку 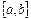 , який розглядається, функція
, який розглядається, функція 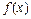 задовольняла наступним вимогам:
задовольняла наступним вимогам:
1. Функція 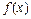 неперервна на відрізку
неперервна на відрізку 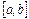 разом з своїми похідними першого і другого порядків.
разом з своїми похідними першого і другого порядків.
2. Значення 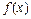 на кінцях ділянки
на кінцях ділянки 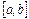 мають різні знаки.
мають різні знаки.
3. Перша і друга похідна f'(x) і f''(x) зберігають певний знак і не перетворюються в нуль на всій дільниці.
Зауважимо, що обмежуємось лише тим випадком, коли корені рівняння додатні. Випадок від'ємних коренів може бути зведений до розгляду додатніх, для чого в рівнянні досить замінити 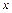 х на
х на 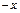 .
.
Спосіб хорд і проведення параболи. Ідея способу хорд полягає в тому, що можна, з певним наближенням, припустити, що функція на досить малій дільниці 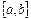 змінюється лінійно. Тоді криву
змінюється лінійно. Тоді криву 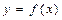 на ділянці
на ділянці 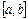 можна замінити хордою і в якості наближеного значення кореня прийняти точку перетину хорди з віссю абсцис.
можна замінити хордою і в якості наближеного значення кореня прийняти точку перетину хорди з віссю абсцис.
Для кращого пояснення способу звернемось до рисунку 3.1.
Побудуємо графік функції 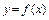 на ділянці
на ділянці 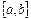 . Істинний корінь рівняння
. Істинний корінь рівняння 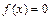 є абсциса точки
є абсциса точки 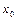 , тобто точка перетину кривої АВ з віссю абсцис. Замінивши криву АВ на хорду АВ, приймаємо в якості наближеного значення кореня точку
, тобто точка перетину кривої АВ з віссю абсцис. Замінивши криву АВ на хорду АВ, приймаємо в якості наближеного значення кореня точку 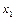 , в якій хорда перетинається з віссю.
, в якій хорда перетинається з віссю.

Рисунок. 3.1- Розв'язок алгебраїчних рівнянь методом хорд 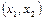 і дотичних
і дотичних 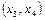 .
.
Знайдемо аналітичний вираз для наближеного значення кореня. Як видно з рисунка 3.1. кутовий коефіцієнт хорди АВ дорівнює
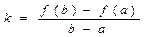 . (3.2)
. (3.2)
Таким чином рівняння хорди АВ можна записати у вигляді
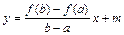 . (3.3)
. (3.3)
Після нескладних перетворень, припустивши, що 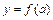 , можна визначити значення
, можна визначити значення 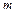 . Тоді
. Тоді
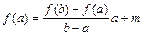 , (3.4)
, (3.4)
звідки
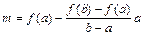 , (3.5)
, (3.5)
і рівняння хорди має вид
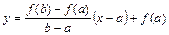 . (3.6)
. (3.6)
Тоді формула наближеного обчислення значення кореня, одержаного по способу хорд, має вид
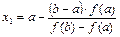 , (3.7)
, (3.7)
або
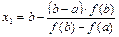 . (3.8)
. (3.8)
Одержане значення 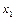 можна знову використовувати для подальшого уточнення кореня способом хорд, розглядаючи інтервал
можна знову використовувати для подальшого уточнення кореня способом хорд, розглядаючи інтервал 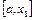 або
або 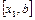 , дивлячись по тому, в якому з них лежить істинний корінь. Щоб визначити це, знаходять знак
, дивлячись по тому, в якому з них лежить істинний корінь. Щоб визначити це, знаходять знак 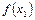 .
.
Більш точно корінь рівняння 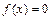 можна одержати, якщо обчислити значення функції
можна одержати, якщо обчислити значення функції 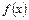 в трьох точках і провести через них параболу, котра краще наближає функцію, ніж хорда. За наближене значення тоді можна взяти точку перетину параболи з віссю
в трьох точках і провести через них параболу, котра краще наближає функцію, ніж хорда. За наближене значення тоді можна взяти точку перетину параболи з віссю  .
.
Спосіб дотичних. Комбінований спосіб. Поряд зі способами хорд і проведення параболи часто використовується інший спосіб, заснований на заміні графіка функції ділянкою прямої лінії.
Звернемось знову до рівняння 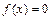 .
.
Візьмемо деяку точку 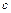 ділянки
ділянки 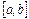 і проведемо в точці
і проведемо в точці 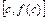 графіка функції дотичну до цього графіка (рисунок 3.1). Рівняння дотичної має вид
графіка функції дотичну до цього графіка (рисунок 3.1). Рівняння дотичної має вид
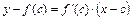 . (3.9)
. (3.9)
В якості наближеного кореня рівняння 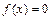 приймемо абсцису точки перетину дотичної з віссю
приймемо абсцису точки перетину дотичної з віссю  . Вважаючи в рівнянні дотичної
. Вважаючи в рівнянні дотичної 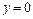 , знаходимо для абсциси точки перетину
, знаходимо для абсциси точки перетину
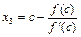 . (3.10)
. (3.10)
Залишається вирішити питання про вибір точки 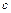 . На рисунку 3.1 прийнято
. На рисунку 3.1 прийнято 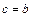 . Неважко переконатись, що в цьому випадку
. Неважко переконатись, що в цьому випадку 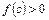 i
i 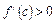 , бо крива ввігнута. Звичайно приймають
, бо крива ввігнута. Звичайно приймають 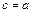 або
або 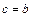 , дивлячись по тому, в якій з цих точок знак функції співпадає з знаком другої похідної, тобто
, дивлячись по тому, в якій з цих точок знак функції співпадає з знаком другої похідної, тобто 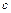 вибирають так, щоб добуток
вибирають так, щоб добуток 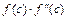 був додатним. В цьому випадку можна гарантувати, що наближене значення кореня, одержане способом дотичних, лежить на ділянці
був додатним. В цьому випадку можна гарантувати, що наближене значення кореня, одержане способом дотичних, лежить на ділянці 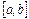 , тобто
, тобто 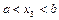 .
.
Як і в способі хорд, значення 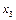 можна використовувати для подальшого уточнення кореня, беручи нову ділянку
можна використовувати для подальшого уточнення кореня, беручи нову ділянку 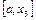 чи
чи 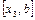 .
.
Спосіб хорд і спосіб дотичних дають наближення кореня з різних сторін (менше і більше істинного кореня). Тому звичайно буває вигідно застосовувати обидва способи одночасно, завдяки чому уточнення кореня може бути одержане швидше.
Спосіб ітерацій. У ряді випадків досить зручним прийомом розв'язку рівнянь є метод ітерацій (повторень). Для застосування такого методу вихідне рівняння повинно бути записане у формі
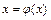 . (3.11)
. (3.11)
Нехай будь-яким чином виділений інтервал 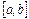 ізоляції кореня цього рівняння, і
ізоляції кореня цього рівняння, і 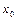 – довільна точка цього інтервалу (нульове наближення). Для одержання наступного наближення
– довільна точка цього інтервалу (нульове наближення). Для одержання наступного наближення 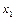 в праву частину рівняння (3.11) замість
в праву частину рівняння (3.11) замість 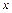 підставляємо
підставляємо 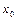 , так що
, так що 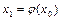 .
.
Дата добавления: 2015-10-09; просмотров: 883;
