РІВНЯННЯ СТАНУ І ЗАКОНИ ПЕРЕНОСУ

Для опису станів макрофізичних властивостей тіл і переносу процесу взаємодії застосовується поняття узагальненого заряду - об’єм, маса і т.д. Розмір заряду в тілі визначає його стан, а перенос його кількісно характеризує процес взаємодії.

Розмір заряду відноситься до екстенсивних величин, тобто до величин, розподілених по об¢єму. Заряд може переноситися під дією узагальненого потенціалу - інтенсивної величини, тобто величини, розподіленої по поверхні. До узагальнених потенціалів відносяться температура, тиск, електричний потенціал, напруга та ін.

Закони переносу визначають залежність між потоками заряду і різницею потенціалів. Закон стану визначає залежність між потенціалом і зарядом. Так, наприклад, для рідких, газоподібних і твердих однорідних тіл заряд - це об’єм, узагальнені потенціали - тиск і температура, рівняння стану - залежність, що виражає зв'язок між об’ємом, тиском і температурою. Залежність між напругами і деформаціями - це механічне рівняння стану.

Якщо потік заряду переноситься в просторі в одному напрямку, то такий перенос називається одномірним, у випадку ж переносу в двох напрямках - плоским, а в трьох напрямках - просторовим.

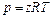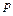Найбільше поширення одержало рівняння Менделєєва - Клапейрона ( , де - тиск, 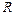- газова стала, 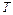- температура, K, 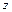- коефіцієнт стисливості).

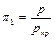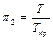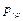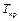Безрозмірний коефіцієнт стисливості залежить від безрозмірного тиску і безрозмірної температури ( і - відповідно критичні тиск і температура).

Для нафтогазової практики, з огляду на точність розрахунків, обумовлену допусками, точністю вихідної інформації, а також точністю контрольно-вимірювальних приладів, коефіцієнт 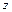можна прийняти рівним одиниці, тобто газ приймається ідеальним. Так, наприклад, для контролю тиску найбільше досконалий засіб - зразкові манометри, похибка яких для деяких манометрів в інтервалів тисків складає +0,35% максимального тиску. Якщо при трубопровідному транспорті газу тиск на початку трубопроводу близько 10 МПа, то застосовується манометр із шкалою 10 МПа, причому похибка буде 0,025 МПа. Урахування коефіцієнта z при порівняно невеликій протяжності газопроводу внесе уточнення не більш зазначеної похибки.

Подамо приклад, що не має прямого відношення до викладу, але добре ілюструє відзначене положення. При трубопровідному транспорті води, з огляду на допуски і точність витратомірів, похибка у визначенні гідравлічних опорів також може досягти декількох відсотків. Часто в інженерних дослідженнях це не враховується. Наприклад, точність розрахованих розмірів не адекватна точності контрольно-вимірювальних приладів. Іноді складають емпіричні рівняння, у яких вплив окремих чинників менше, ніж точність, із якою маже бути визначена функція. Надаючи велике значення цьому питанню, в спеціальному параграфі зроблено стислий виклад теорії помилок, в основному маючи на увазі їхнє прикладне значення для нафтогазопромислової механіки.

Подамо рівняння стану рідини, що часто застосовується в нафтогазопромисловій механіці для баротропної рідини,

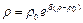, (4.1)

де 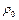- густина при тиску 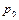, 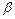- коефіцієнт об'ємного пружного розширення рідини.

Дане рівняння може бути апроксимовано лінійною залежністю

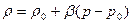. (4.2)

Відзначене справедливо для так званих малостисливих рідин. Дуже часто, ідеалізуючи рівняння, не вказують умови, при котрих ця ідеалізація може використовуватись практично.

Так, в аналізованому випадку тільки по коефіцієнта пружного розширення рідини не можуть бути віднесені до малостисливих. Це залежить і від інтервалу зміни тиску, тобто якщо є дві рідини й в одної коефіцієнт 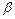менший, ніж в іншої, це не свідчить про можливість застосування лінійної апроксимації. Необхідно звернути увагу на інтервал зміни тиску.

Розглянемо критерії, що дозволяють з'ясувати умови, при яких варто враховувати пружність і стисливість рідини. Так, наприклад, при нестаціонарному русі в’язкої рідини в довгому трубопроводі, а також у пористому середовищі доцільно застосувати поняття часу релаксації (ослаблення стану тіла після припинення впливу, що викликав цей стан). Оцінимо порядок часу релаксації для руху в трубопроводі. Під порядком розуміється порядок розміру: секунди, десятки секунд, сотні секунд і т.д. Час релаксації буде залежати від сили інерції, обумовленою масою (густиною) і в¢язкістю. Тому що розвиток профілю швидкостей залежить в основному від радіуса, отже,

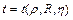. (4.3)

Неважко бачити, що з цих чотирьох розмірів може бути складений один безрозмірний параметр.

Подана залежність рекомендується у виді степеневої комбінації, що можливо при одному безрозмірному параметрі

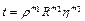. (4.4)

Користуючись розмірністю величин, що входять в останнє рівняння, одержуємо

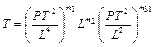, (4.5)

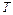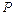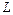де , і - відповідно розмірності часу, сили і довжини.

У лівій і правій частині рівняння розмірності повинні бути однакові (однорідність розмірності). У лівій частині відсутн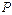і і 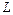, точніше, вони входять у нульовому степені. Отже, і в правій частин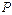і і 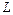повинні бути в нульовому степені, 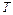– в першому, тобто

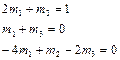. (4.6)

Звідси ; ; .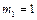

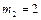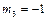Таким чином,

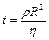. (4.7)

Час релаксації має порядок .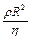

Подамо чисельний приклад. Через 4" трубопровід прокачується в¢язка нафта густиною 0,8 г/см³ і в¢язкістю 5 сП. Тоді

.

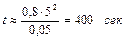Таким чином, час релаксації порядку декількох хвилин.

Якщо робочий період трубопроводу більше часу релаксації, то можна зневажити пружністю рідини і розглядати рух як стаціонарний. При дослідженні пускового періоду трубопроводу, час котрого співрозмірний з часом релаксації, необхідно розглядати нестаціонарний рух.

Для твердого скелета пружного пористого середовища приймається таке рівняння стану:

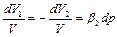, (4.8)

де 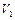- об’єм порового простору; 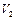- об’єм рідини; 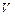- початковий об’єм; 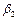- коефіцієнт стисливості.

Строго говорячи, 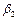не коефіцієнт стисливості, тому що в приведену формулу входить зміна порового простору, а не зміна об’єму твердого скелета. Експериментальні ж дослідження показують, що ці розміри мало відрізняються.

Перейдемо до розгляду різноманітних рівнянь переносу маси (закон Дарсі і Фіка), тепла (закон Фур'є), електричного струму (закон Ома).

Докладно викладемо, як експериментальним шляхом установлений закон переносу маси в пористому середовищі - закон Дарсі. Розглянемо рух практично нестисливої рідини. Введемо поняття фіктивної середньої швидкості, тобто коли потік рідини розподілений по всьому перерізі твердого скелета і пір. Швидкості і прискорення змінюються як за величиною, так і за напрямком пористого середовища. Через велику розмаїтість пір неможливо врахувати швидкість окремих часток. Прийнято розглядати значення швидкостей у деякому об’ємі. Практична нестисливість рідини перевіряється рівністю витрат при вході і виході, при цьому мається на увазі рівність у межах похибки застосовуваних витратомірів. Таким чином, у даному випадку заряд може бути схарактеризований швидкістю фільтрації. При безінерційній фільтрації характерним буде перепад тиску, віднесений до одиниці довжини. Так, наприклад, знаючи перепад тиску при заданій витраті на заданій довжині, можна визначити перепад тиску на будь-якій довжині. Відзначене не відноситься до стисливої рідини, так як у цьому випадку розподіл тиску по довжині не буде носити лінійного характеру. В міру віддалення від входу тиск падає, що при незмінності масової витрати призводить до збільшення об'ємної витрати. На рисунку 4.1 подані три залежності розподілу тиску.

Процес фільтрації нестисливої рідини характеризується прямою лінією 1. Порівняємо випадки фільтрації стисливої і нестисливої рідин (порівнюються рідини, що мають однакові густини при однакових об'ємних витратах і тисках на вході). Об'ємна витрата в міру віддалення від початку відліку росте для стисливої рідини, у результаті чого тиск наприкінці відліку (точка В) нижче тиску нестисливої рідини (точка А).

Рисунок 4.1 – Процеси фільтрації рідини.

Розглянемо, по який із кривих (2 або 3) повинна відбутися зміна тиску. В міру віддалення від початку відліку перепад тиску повинен збільшуватися через безупинне збільшення витрати (крива 2). По кривій 3 інтенсивність перепаду тиску зменшується.

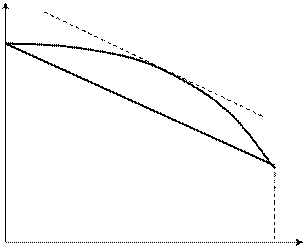
Для більшої фізичної ясності розглянемо інший приклад, коли тиск на початку і наприкінці відліку для стисливої і нестисливої рідин однаковий. В міру віддалення від початку відліку витрата для стисливої рідини буде рости, залишаючись меншою, ніж для нестисливої. У деякій точці М (рисунок 4.2) витрати нестисливої і стисливої рідин будуть одинакові, після чого витрата для стисливої, рідини буде більше, ніж для нестисливої. До точки М інтенсивність зміни тиску для стисливої рідини буде більшою, ніж для нестисливої, у точці М вони рівні, а потім інтенсивність зміни тиску стисливої рідини буде менше інтенсивності нестисливої. Тому що інтенсивність зміни тиску характеризується похідною, то в точці М дотична, проведена до кривої, буде рівнобіжна прямій, проведеній для стисливої рідини.

p

М

0 L x

Рисунок 4.2 – Зміна тиску для різних рідин.

Отже (див. рис. 3.2), при русі стисливої рідини крива розподілу тисків звернена увігнутістю до осі абсцис. Це відноситься до стаціонарної фільтрації, коли величини, що характеризують фільтрацію, практично незмінні у часі.

Стан систем термодинаміки характеризується узагальненим зарядом. Якщо заряд знаходиться в статичному стані і не змінюється у часі, то система є стаціонарною, рівноважною (статика). Пронизування системи незмінним зарядом відповідає стаціонарно нерівноважній системі (кінетика). При заряді, що змінюється, але не пронизує систему, система нестаціонарно рівноважна (статс-динаміка). І, нарешті, для нестаціонарно нерівноважної системи (кінете-динамика) відбувається перенос заряду й одночасна зміна в часі.

Тому що будемо розглядати безінерційну фільтрацію, то густина не характеризує даний процес. Отже, швидкість фільтрації w визначається такою функціональною залежністю:

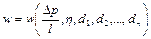, (4.9)

де 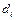- діаметри зерен, що складають пористе середовище.

На підставі π-теореми можна записати

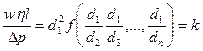. (4.10)

Розмір 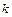, що стоїть у правій частині і характеризує пористе середовище та залежить від його складу, називається проникністю. Вона має розмірність квадрата довжини і визначається дослідним шляхом. На перший погляд, приведений закон переносу (закон Дарсі) установлений лише тільки на основі застосування π-теореми. Але це не так: π-теорема дозволяє лише ощадливо пізнати процес. У даному випадку безінерційність руху перевіряєтся експериментально на основі того, що залежність між 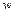і 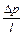прямолінійна.

У диференційній формі закон Дарсі може бути записаний у виді

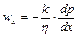. (4.11)

У цьому випадку розглядається одномірний рух уздовж осі 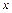. Вздовж осі 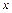тиск зменшується і 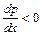. У правій частині поставлений знак мінус, тому що швидкість фільтрації, спрямована уздовж осі 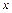, позитивна. Для просторової фільтрації в ізотропному пористому середовищі:

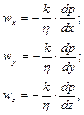(4.12)

або

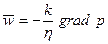. (4.13)

Закон Дарсі може бути витлумачений як лінійний закон опору в рівняннях руху. При дослідженні стаціонарних рухів застосовується закон опору, одержаний для стаціонарних прямувань, тобто застосовується принцип квазістаціонарності. Відзначене, мабуть, справедливо для процесів, що протікають у часі порівняно повільно.

Час релаксації нестаціонарних процесів, що відбуваються в пористому середовищі у результаті стисливості рідини і скелета, характеризується коефіцієнтом п¢єзопровідності, що має розмірність см²/с,

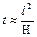, (4.14)

де 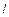- характерний розмір.

Так, для однієї свердловини, розташованої в пласті, на якому свердловини и розміщені по 200-метровій сітці 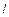може бути прийнято рівним половині відстані між свердловинами, тобто 100 м.

Для пласту проникністю 0,25 Д, при коефіцієнті пружної ємності 3×10^-5 і фільтрації рідини в¢язкістю 7,5 сП H = 10⁴ см²/с. Тоді

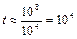с.

Таким чином, час релаксації буде біля 3 год, тобто нестаціонарність становить інтерес для короткочасного дослідження свердловин, тобто таких досліджень, час котрих дорівнює декільком годинам. Для розробки пластів, коли час обчислюється роками, нестаціонарність можна не враховувати. Для великих 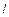, що характеризують розмір пласту, наприклад 10 км,

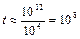с,

тобто час релаксації буде біля 3 років. Для розробки такого порівняно значного покладу нестаціонарність необхідно враховувати.

Відзначене відноситься і до випадків прикладання навантажень статичної і динамічної, для яких напруження залежить не тільки від пружної деформації, але і від її швидкості. Динамічні розрахунки з урахуванням нерівноважності процесу являють великий інтерес для нафтогазопромислової механіки, особливо для нових методів впливу на пласт. Проте вони не одержали належного розвитку. Закон Дарсі справедливий в області лінійної фільтрації. Для нелінійної фільтрації знаходять застосування степеневі закони. Звичайно ці закони записуються для одномірних випадків.

Явище переносу тепла відзначається у всіх ланках буравлення, нафтовидобутку і транспорту й описується законом Фур'є

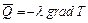, (4.15)

де 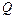- густина теплового потоку; 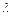- коефіцієнт теплопровідності; 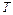- температура.

Це рівняння, як і всі приведені вище, ставиться до однорідного й ізотропного середовища, для яких коефіцієнти проникності, дифузії і теплопровідності однакові у всіх напрямках (ізотропність) і у всіх точках (однорідність).

Для нафтогазопромислової механіки подає великий інтерес і закон переносу електричного струму, як для розрахунку деяких процесів, наприклад електрокаротажна, електропідігрівачів та ін., і в основному для методу електричних аналогій.

Закон переносу електричного струму - закон Ома - має вид

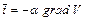, (4.16)

де 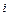- густина електричного струму; 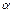- коефіцієнт пропорційної електропровідності; 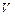- потенціал.

Неважко зауважити аналогію між законами Дарсі, Фур'є і Ома.

Для приведених законів густина потоку, що відповідає фільтрації і швидкості, пропорційна градієнту узагальненого потенціалу.