Методи побудови регресійних моделей

Введемо наступні позначення: Y – вектор вихідних змінних сис­теми, що моделюються; X – вектор вхідних параметрів, які контролюю­ться.

В постановці задачі регресійного аналізу y_i – деяка випадкова ве­личина, яка змінюється навколо невідомого параметру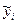

,

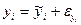де 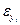- випадкова флуктуація.

Як правило регресійна модель зв¢язує два параметри. Щоб побудувати регресійну модель, необхідно встановити факт існування зв¢язку між досліджуваними параметрами, який підтверджується кореляційним моментом (коваріацією). З точки зору статистики коваріація може бути визначена

,

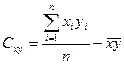де 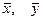- математичне очікування значення змінних х і у.

Величина коваріації дозволяє знайти коефіцієнт кореляції

,

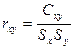де 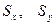- середньоквадратичні похибки у визначенні змінних х і у.

Вважають, що, якщо 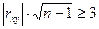, то зв¢язок між випадковими величинами х і у досить імовірний. В такому випадку можна побудувати рівняння регресії у вигляді

.

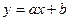Нехай в площині ХОУ маємо набір точок 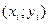. Ці точки, як правило, не лежать на одній прямій лінії в силу випадковості вимірювань, тому формула рівняння регресії є наближеною (рис.6.5).

Рисунок 6.5 – Лінія регресії

Задача зводиться до визначення коефіцієнтів а і b. Найпростіше це зробити за методом найменших квадратів, суть якого полягає в тому, що треба вибрати таку лінію, сума квадратів віддалей усіх точок від якої буде мінімальною. Згідно з цим методом мінімізуємо суму

.

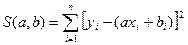Тут 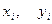- задані числа.

Щоб мінімізувати суму знаходимо похідні

; .

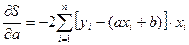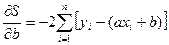Прирівнюючи ці похідні до нуля, одержимо систему рівнянь для визначення коефіцієнтів а і b

,

,

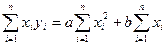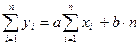звідки

; .

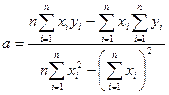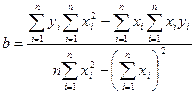Для оцінки точності регресійного аналізу визначають середньоквадратичну похибку і коефіцієнт варіації.