АНАЛІЗ РОЗМІРНОСТЕЙ І МЕТОД АНАЛОГІЙ

Аналіз розмірностей, теорія подоби, моделювання, а також метод аналогії різноманітних явищ дозволяють, поряд із правильною постановкою і проведенням експериментів, прискорити обчислювальні й інші роботи. Проте в теоретичних основах транспорту нафти і газу цей метод широко не застосовується. У той же час у теоретичних основах розробки нафтових і газових покладів ці засоби порівняно широко застосовуються.

Для правильної постановки експериментів, опрацювання одержуваних результатів і узагальнень потрібно проводити кількісно-теоретичний аналіз. У цьому випадку зменшується кількість дослідів, результати яких виражаються в безрозмірних параметрах. У гідродинаміці, зокрема, ці параметри визначаються, як співвідношення сил.

Звичайно розрізняють величини розмірні і безрозмірні. Прикладами розмірних величин є швидкість, тиск, в’язкість, гранична напруга зсуву, довжина, час і ін.

Відношення довжини до її діаметра, сил в’язкісті до граничної напруги зсуву і т.д. є безрозмірними величинами. Аналіз теорії розмірностей дозволяє у рівняннях шляхом переходу від розмірних змінних до безрозмірним зменшити число змінних. Припустимо, що дане таке квадратне рівняння

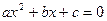, (5.1)

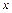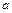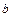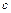де безрозмірний залежить від коефіцієнтів , і , що мають однакові розмірності.

Якщо всі члени рівняння розділити на 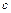, то рівняння прийме вид

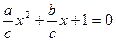. (5.2)

Як очевидно з рівняння, перемінна 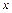залежить від 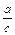і 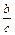, тобто .

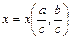Отже, запис рівняння в безрозмірному виді дозволяє зменшити число змінних із трьох до двох.

Якщо рівняння невідомо або необхідно визначити вид функціональної залежності, то замість зміни 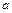і 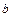змінним відношення 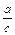і 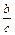. Таким чином, не тільки зменшується число змінних, але і при найменших витратах часу і праці досягається можливість проведення експерименту.

Припустимо, що для постановки експерименту потрібна зміна величин 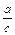і 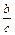. Якщо під час експериментування величину с легко змінити, то, змінивши розмір 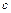, можна змінити розміри 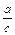і 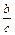(при цьому розміри 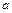і 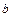залишаються постійними), і, навпаки, якщо важко змінити розмір 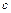при експериментуванні, то, змінивши величини 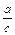і 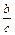можна змінити величини 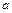і 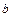. Якщо ж при проведенні експериментів складно змінити розміри 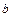і 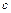то зміною однієї з них можна досягти зміни відношення величин.

Фізичні основи зв'язують величини визначеними залежностями. Тому, якщо для деяких величин будуть вибрані розмірності, то на підставі відповідних формул можуть бути отримані розмірності інших величин. Залежність між фізичними величинами дозволяє вибрати таку основну систему розмірностей, що для виміру в цій системі механічних величин достатній довільний вибір трьох розмірностей.

У багатьох випадках у техніці одиниці довжини L, часу Т і сили F приймаються за основні одиниці. Проте серед одиниць виміру в’язкість h, швидкість v і густина r також можуть бути прийняті за основні. Такі величини називаються величинами із незалежними розмірностями (див. нижче).

В даний час прийнята міжнародна система одиниць СІ, у якій розмірність довжини 1 м, маси – 1 кг і часу - 1 с.

Якщо позначити незалежні розмірності довжини, часу і сили відповідно через L, Т и F, то широко застосовувані в гідромеханіці розміри будуть мати такі розмірності:

швидкість

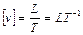; (5.3)

прискорення

;

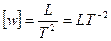кутова швидкість

;

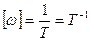в’язкість

;

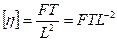гранична напруга зсуву

;

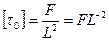тиск

;

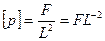густина

;

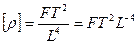питома вага

;

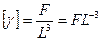маса

.

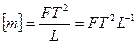Якщо для математичного опису не можна скласти диференційне рівняння або іншу математичну залежність, то, застосовуючи теорію розмірностей, можна описати фізичне явище без рівняння, що описує процес. Але для цього необхідно знати початкові і граничні умови, що пояснюють дане явище. Застосування для цих цілей π-теореми (теореми Букінгема) дозволяє виявити основні безрозмірні параметри, що характеризують аналізоване явище.

Припустимо, що безрозмірна величина а залежить від незалежних одна від одної змінних величин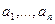

.

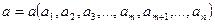Функціональна залежність звичайно записується у виді 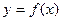; при великій кількості залежностей 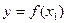; 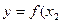) і т.д. Знаки функції повинні прийматися різними. Простіше залежності зображуються так: 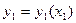; ; 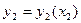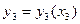і т. д.

Припустимо, що серед цих розмірних величин число величин із незалежними розмірностями дорівнює m. У механіці і техніці їх не може бути більше трьох. За незалежні розмірності приймаються довжина L, час Т, сила F або ж їхня степенева комбінація, із якої можуть бути отримані L, Т и F, наприклад:

;

;

.

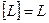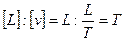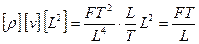У рівняння входять п + 1 розмірних величин. На підставі π-теореми зв'язок між n + 1 розмірними одиницями може бути здійснений 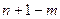безрозмірними параметрами, що складаються з п + 1 розмірних величин.

Тоді безрозмірні параметри можна записати

;

;

..........................................

..........................................

.

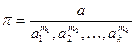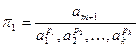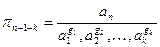Тут показники 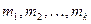; ; 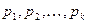; 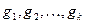вибираються так, щоб параметри 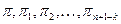одержались у безрозмірному виді.

Застосування π-теореми пояснимо на конкретному прикладі. Припустимо, що замість величини а дана Δр, а замість величин із незалежними розмірностями дані v, ρ, l. Тоді одержимо

.

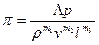Тому що в цій формулі ліва частина (L⁰, F⁰, Т⁰) безрозмірна то і права частина повинна бути безрозмірною, тобто

.

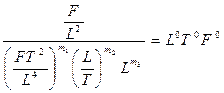Тоді, прирівнюючи показники степеня при L, Т и F, одержуємо:

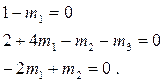
Розв¢язок цієї системи трьох лінійних рівнянь буде таким:

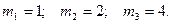
Отже, безрозмірний параметр можна подати у виді

.

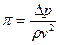Цей вираз являє собою відношення тиску й інерції і називається параметром Эйлера.

При використанні теорії розмірності використовуються фізичні і математичні розуміння.

Роздивимося стаціонарний рух нестисливої в¢язко-пластичної рідини в циліндричній трубі. Перепад тиску на кінцях трубопроводу залежить від довжини і діаметра труби, структурної в’язкості, граничної напруги зсуву, густини рідини, а також прискорення від сили ваги і швидкості руху. При русі стисливої рідини у рівняння повинен увійти не перепад тиску, а абсолютні значення тисків, що діють на кінцях труби. Для аналізованого випадку фізичне рівняння має вид

,

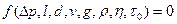або

.

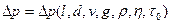Тому що число незалежних дорівнює трьом, то, використовуючи π-теорему, можемо вивести п'ять безрозмірних параметрів. У даному випадку в якості величин із незалежними розмірностями можуть бути обрані такі: 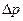, d і v; g, l і 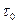та ін.

Вище було відзначено, що в кожному варіанті величини з незалежними розмірностями потрібно вибирати так, щоб їхні степеневі комбінації дали б можливість одержати розмірності довжини L, сили F, часу Т. Тепер для прийнятих варіантів перевіримо цю умову.

Тому що в першому варіанті тиск, діаметр і швидкість прийняті за основні, то, комбінуючи їх, будемо прагнути одержати розмірності L, F і Т. Знайдемо розмірність довжини

;

,

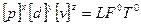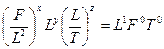звідки

.

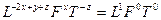Отже,

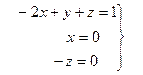
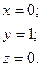
Таким чином, для одержання розмірності довжини потрібно прийняти таку комбінацію р, d і v.

.

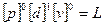Знайдемо розмірність сили:

;

.

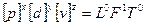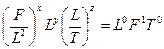звідки

.

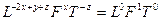Отже,

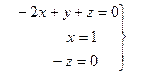
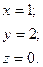
тобто для одержання розмірності сили потрібно скористатися такою комбінацією р, d і v.

.

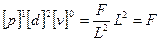Знайдемо розмірність часу

;

,

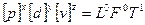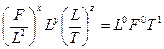звідки

.

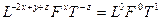Отже,

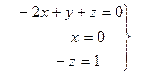
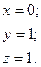
Розмірність часу одержимо з приведеної нижче комбінації р, d і v.

.

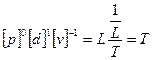У кожному варіанті комбінації цих величин вибираються так, щоб у результаті можна було б одержати безрозмірний параметр.

Тепер покажемо прикладне застосування теореми.

Розглянемо процес руху в¢язкої рідини в циліндричній трубі. В якості основних параметрів процесу і характеристик системи виберемо густину ρ , в¢язкість рідини η , витрату рідини q , втрату тиску Δр, діаметр трубопроводу d і його довжину l. Крім того, у число визначаль­них факторів необхідно ввести прискорення сили ваги g, так як гравіта­ція впливає на рух рідини. Таким чином, для опису процесу вибрано 7 незалежних параметрів. Вони включають 3 розмірні категорії: розмір­ність маси [M], розмірність часу [T] і розмірність довжини [L].

Таким чином, на основі π-теореми необхідно одержати 7 – 3 = 4 визначальні безрозмірні комплекси. З цією метою з числа визначальних параметрів необхідно вибрати три незалежні, які включали б у себе всі три розмірні категорії і не утворювали безрозмірної групи. В якості таких параметрів виберемо в¢язкість μ, густину рідини ρ і діаметр труби d. Легко переконатись у тому, що вони включають усі розмірні катего­рії. Щоб переконатись у тому, що вони не утворюють безрозмірної групи, складемо матрицю

.

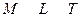
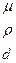
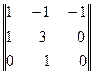Цифри матриці указують, у якому степені дана розмірна категорія присутня у розмірності параметра.

Детермінант системи

.

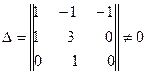Той факт, що детермінант системи не рівний нулю, говорить про те, що дані параметри не утворюють безрозмірної групи.

Тепер подамо кожний з параметрів процесу, що залишилися, в виді відношень (π-параметрів)

; ;

; .

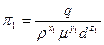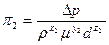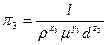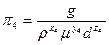Виберемо показники степеня 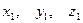таким чином, щоб пер­ший π-параметр був безрозмірною величиною. Для цього необхідно за­довольнити умову

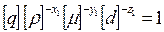
або

.

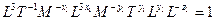Звідси одержимо систему рівнянь

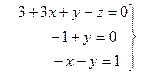
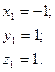
Тепер перший член π₁ подається в вигляді

.

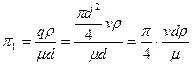Постійний множник 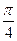може бути опущений. Тоді перший π₁-член є відомим критерієм Рейнольдса

.

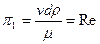Міркуючи аналогічним чином, одержимо для другого члена вираз

,

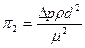для третього члена

,

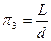для четвертого члена

.

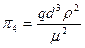Враховуючи, що 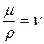- кінематична в¢язкість, одержимо

; .

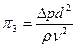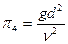Тепер розглянемо вихідну залежнісь

.

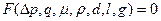З врахуванням одержаних π-параметрів ця залежність може бути подана у вигляді

.

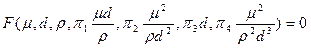Відзначимо, що вид залежності не залежить від вибору системи оди­ниць. Тому можна припустити, що вибрані незалежні параметри є одиницями вимірювань, тобто

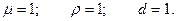
Тоді маємо

,

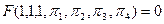або

.

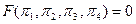Таким чином, вид шуканої функції цілком визначається знайде­ними π-параметрами. Якщо в вихідній постановці задачі потрібно було знайти залежність між сімома розмірними величинами, то в кінцевому резуль­таті задача пов¢язана з відшукуванням залежності між чотирма парамет­рами.