Закон збереження маси
У цьому параграфі розглядається вивід рівняння нерозривності для різних випадків руху однорідної і неоднорідної рідини, який є математичним виразом закону збереження (постійності) маси. У загальному випадку руху швидкість 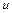 , густина
, густина 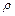 і тиск
і тиск 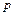 є функції координат
є функції координат  ,
, 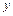 і
і 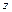 , частинки, що рухається, і часу
, частинки, що рухається, і часу 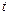 , тобто
, тобто
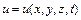 ; (2.18)
; (2.18)
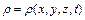 ; (2.19)
; (2.19)
 . (2.20)
. (2.20)
При цьому 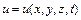 - швидкість рідини у кожній даній точці простору у момент часу
- швидкість рідини у кожній даній точці простору у момент часу 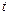 , тобто вона відноситься до певних точок простору, а не до певних частинок рідини, які рухаються у просторі. Теж саме відноситься до
, тобто вона відноситься до певних точок простору, а не до певних частинок рідини, які рухаються у просторі. Теж саме відноситься до 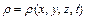 і
і 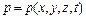 .
.
Нестислива рідина.
Розглядається одномірний рух рідини у трубі (рисунок 2.3.) вздовж осі  .
.
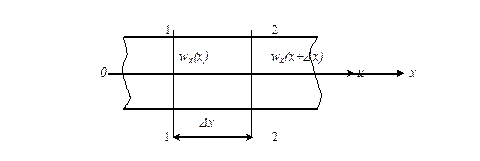
Рисунок 2.3 – Схема одномірного руху рідини у трубі.
Рахуючи, що рідина нестислива, приймаємо, що у ній неможливе утворення пустот, тобто дотримується умова нерозривності руху. Виходячи з цього, кількість рідини, яка проходить за одиницю часу через переріз 1 – 1 ( 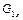 ) і 2 – 2 (
) і 2 – 2 ( 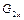 ) повинна бути рівною, тобто
) повинна бути рівною, тобто
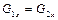 . (2.21)
. (2.21)
Позначимо через 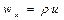 масову швидкість у напрямі осі
масову швидкість у напрямі осі  , де
, де 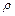 - густина рідини, яка розглядається. Так як маса рідини в об'ємі, який розглядається, не змінюється, то масова швидкість у всіх перерізах буде однакова
- густина рідини, яка розглядається. Так як маса рідини в об'ємі, який розглядається, не змінюється, то масова швидкість у всіх перерізах буде однакова
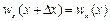 . (2.22)
. (2.22)
Отже
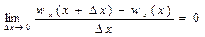 , (2.23)
, (2.23)
тобто
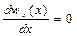 . (2.24)
. (2.24)
Формула (2.14) виражає закон збереження маси при одномірному русі рідини. Виходячи з формули (2.13) чи (2.14) маємо 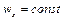 , тобто із врахуванням постійності густини
, тобто із врахуванням постійності густини 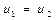 , де
, де 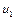 – середня швидкість у перерізі 1 – 1, а
– середня швидкість у перерізі 1 – 1, а 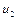 - у перерізі 2 – 2.
- у перерізі 2 – 2.
При виводі рівняння (2.14) передбачається, що площа перерізу труби постійна. У іншому випадку, позначаючи площу перерізу 1 – 1 через 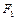 , а площу 2 – 2 через
, а площу 2 – 2 через 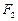 і враховуючи, що
і враховуючи, що
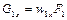 і
і 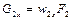 (2.25)
(2.25)
з формули (2.12) одержимо
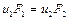 . (2.26)
. (2.26)
З формули (2.16) видно, що при усталеній течії нестисливої рідини середні швидкості у поперечних перерізах обернено пропорційні до площ цих перерізів.
Так як при усталеній течії газу масова витрата по довжині труби має одне і те саме значення, то, виходячи з (2.12) і (2.15), для усталеної течії газу одержуємо
 (2.27)
(2.27)
або
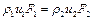 . (2.28)
. (2.28)
Розглянемо випадок плоскої течії нестисливої рідини. Для цього візьмемо паралелепіпед з сторонами 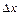 ,
,  , 1 об'ємом
, 1 об'ємом 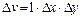 (рисунок 2.4).
(рисунок 2.4).
Кількість рідини, яка перетікає через сторони 1, 2, 3 і 4, відповідно буде
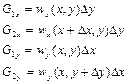 , (2.29)
, (2.29)
де 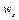 і
і 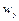 – масові швидкості у напрямі осей
– масові швидкості у напрямі осей 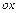 і
і 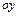 .
.
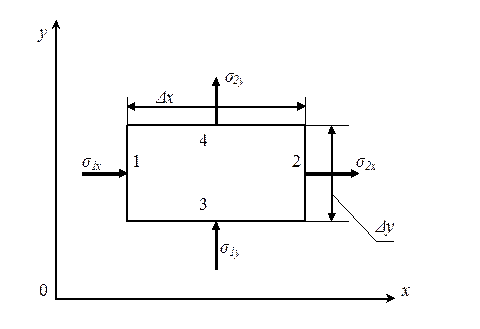
Рисунок 2.4 – Схема плоскої течії рідини.
Відзначимо, що на рисунку 2.4 не обмежуємо напрям течії. Рідина може надходити через грані 1 і 4 і витікати через грані 2 і 3 або надходити через грані 1 і 2 і витікати через грані 3 і 4. Також можливі інші напрями течії. Але кількість рідини, що надійшла, повинна бути рівною кількості рідини, яка витекла. Це пояснюється тим, що у розглянутому прикладі рідина нестислива, тобто у об'ємі, який розглядається, маса (густина) рідини не змінюється.
Іншими словами,
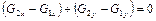 . (2.30)
. (2.30)
Закон збереження маси (2.18) показує, що кількість рідини, яка надійшла у даний об'єм, рівна кількості рідини, яка витекла з даного об'єму. Вирази у дужках у формулі (2.18) завжди мають різні знаки, причому тут приводяться алгебраїчні значення 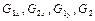 . Останнє зауваження має місце при будь-якому варіанті течії.
. Останнє зауваження має місце при будь-якому варіанті течії.
Зміна кількості рідини у прямокутнику, який розглядається, буде
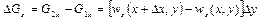 (2.31)
(2.31)
у напрямі осі 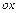 і
і
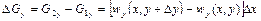 (2.32)
(2.32)
у напрямі осі 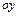 .
.
У всіх випадках течії нестисливої рідини 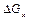 і
і 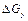 будуть мати різні знаки і
будуть мати різні знаки і
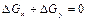 . (2.33)
. (2.33)
Формула (2.21) одержана з врахуванням рівності кількості рідини, яка надходить у розглянутий об'єм, до кількості рідини, яка витікає з цього об'єму. Підставивши значення 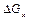 і
і 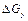 з (2.19) і (2.20) у (2.21) одержуємо
з (2.19) і (2.20) у (2.21) одержуємо
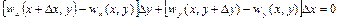 . (2.34)
. (2.34)
Розділивши останній вираз на 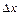 ,
,  і перейшовши до границі
і перейшовши до границі 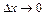 і
і 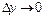 , одержимо
, одержимо
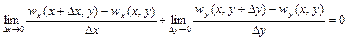 (2.35)
(2.35)
або
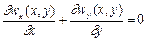 . (2.36)
. (2.36)
Формула (2.22) виражає закон збереження маси і називається рівнянням нерозривності (суцільності) при плоскій течії нестисливої рідини.
У формулі (2.22) 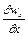 і
і 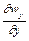 завжди мають різні знаки. Це пояснюється тим, що якщо, наприклад,
завжди мають різні знаки. Це пояснюється тим, що якщо, наприклад, 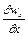 від'ємна величина, то
від'ємна величина, то 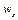 зменшується, і у напрямі осі
зменшується, і у напрямі осі 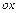 більше надходить рідини (через переріз 1), ніж витікає (через переріз 2), що може призвести до нагромадження рідини. Тому з-за нестисливості рідини у напрямі
більше надходить рідини (через переріз 1), ніж витікає (через переріз 2), що може призвести до нагромадження рідини. Тому з-за нестисливості рідини у напрямі 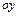 витік рідини повинен бути більше її притоку.
витік рідини повинен бути більше її притоку. 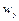 буде рости вздовж
буде рости вздовж 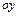 , тобто значення
, тобто значення 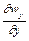 повинно бути додатним. Точно також при додатному
повинно бути додатним. Точно також при додатному 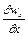 витік рідини у напрямі
витік рідини у напрямі 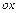 повинен компенсуватися її притоком у напрямі
повинен компенсуватися її притоком у напрямі 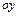 , отже
, отже 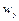 буде зменшуватись, тобто значення
буде зменшуватись, тобто значення 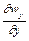 повинно бути від'ємним.
повинно бути від'ємним.
Нарешті, розглянемо течію нестисливої рідини у просторі. Для цього візьмемо паралелепіпед (рисунок 2.5), грані якого паралельні координатним площинам і мають площі відповідно
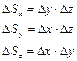 . (2.37)
. (2.37)
Кількість рідини, яка протікає через грані взятого паралелепіпеда, визначається за формулами
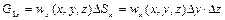 ; (2.38)
; (2.38)
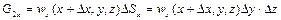 ; (2.39)
; (2.39)
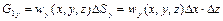 ; (2.40)
; (2.40)
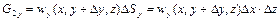 ; (2.41)
; (2.41)
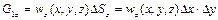 ; (2.42)
; (2.42)
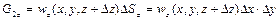 . (2.43)
. (2.43)
де 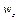 – масова швидкість у напрямі осі
– масова швидкість у напрямі осі 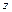 .
.

Рисунок 2.5 – Течія нестисливої рідини у просторі.
Зміна кількості рідини у розглядуваному паралелепіпеді буде:
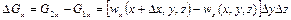 (2.44)
(2.44)
у напрямі 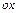 ;
;
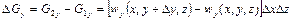 (2.45)
(2.45)
у напрямі 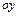 ;
;
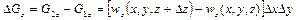 . (2.46)
. (2.46)
Так як рідина нестислива, то
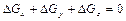 . (2.47)
. (2.47)
У залежності від напряму руху дві з цих величин будуть мати однаковий знак, а третя величина – протилежний. У іншому випадку рідина з усіх сторін буде надходити у об'єм, який розглядається, що фізично неможливо з-за нестисливості рідини.
Підставивши значення 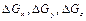 у (2.23), розділивши їх відповідно на
у (2.23), розділивши їх відповідно на 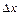 ,
,  і
і  та перейшовши до границі
та перейшовши до границі 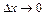 ,
, 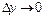 і
і 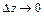 , одержимо
, одержимо
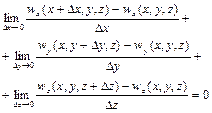 , (2.48)
, (2.48)
або
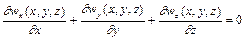 . (2.49)
. (2.49)
Формула (2.24) виражає закон збереження маси і називається рівнянням нерозривності (суцільності) при просторовій течії нестисливої рідини. При одержанні рівняння (2.24) припускається, що рідина нестислива, тобто маса (густина) рідини у об'ємі, який розглядається, не змінюється. Якщо у (2.24) значення 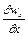 і
і 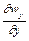 мають однаковий знак, наприклад додатний, то це означає, що у напрямі
мають однаковий знак, наприклад додатний, то це означає, що у напрямі 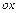 і
і 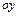 більше витікає рідини, ніж надходить, так як у цьому випадку
більше витікає рідини, ніж надходить, так як у цьому випадку 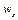 і
і 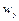 зростають. У зв'язку з нестисливістю рідини цей витік повинен компенсуватися притоком у напрямі
зростають. У зв'язку з нестисливістю рідини цей витік повинен компенсуватися притоком у напрямі 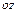 . По напряму
. По напряму 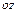 приток рідини у об'єм, який розглядається, повинен бути більше її витоку з цього об'єму, тобто
приток рідини у об'єм, який розглядається, повинен бути більше її витоку з цього об'єму, тобто 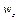 буде зменшуватись, отже, значення
буде зменшуватись, отже, значення 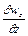 повинно бути від'ємним.
повинно бути від'ємним.
Стислива рідина.
Якщо рідина стислива, тобто густина (і, відповідно, маса) рідини може змінюватись у часі, то зміна кількості рідини у розглянутому об¢ємі призведе до зміни густини (маси) рідини у тому ж об¢ємі. Так, наприклад, для стисливої рідини (рисунок 2.3) 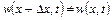 і за деякий проміжок часу
і за деякий проміжок часу 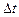 різниця між кількістю притоку рідини у даний об’єм і відпливу з нього призведе до зміни густини рідини у аналізованому об¢ємі. При цьому якщо
різниця між кількістю притоку рідини у даний об’єм і відпливу з нього призведе до зміни густини рідини у аналізованому об¢ємі. При цьому якщо 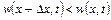 , тобто у даний об’єм більше притікає рідини, чим із нього випливає, то це призведе до збільшення густини у даному об¢ємі, якщо ж
, тобто у даний об’єм більше притікає рідини, чим із нього випливає, то це призведе до збільшення густини у даному об¢ємі, якщо ж 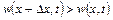 , то кількість рідини, що випливає з даного об¢єму, більше кількості рідини, що притікає у нього і призведе до зменшення густини рідини у даному об’ємі. Таким чином, якщо протягом деякого проміжку часу
, то кількість рідини, що випливає з даного об¢єму, більше кількості рідини, що притікає у нього і призведе до зменшення густини рідини у даному об’ємі. Таким чином, якщо протягом деякого проміжку часу 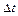 величина
величина 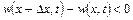 , то густина у даному об’ємі зростає, тобто
, то густина у даному об’ємі зростає, тобто  , якщо ж
, якщо ж  , то густина у даному об’ємі зменшується, тобто
, то густина у даному об’ємі зменшується, тобто 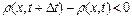 .
.
Отже, зростання масової швидкості 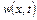 у даному об’ємі за деякий проміжок часу
у даному об’ємі за деякий проміжок часу  призводить до зменшення густини рідини у даному об’ємі, а зменшення масової швидкості призводить до зростання густини у даному об’ємі. Іншими словами,
призводить до зменшення густини рідини у даному об’ємі, а зменшення масової швидкості призводить до зростання густини у даному об’ємі. Іншими словами, 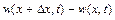 і
і 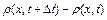 завжди будуть мати протилежні знаки, тобто знаки
завжди будуть мати протилежні знаки, тобто знаки 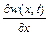 і
і 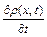 - будуть різні. Таким чином, якщо для нестисливої рідини
- будуть різні. Таким чином, якщо для нестисливої рідини 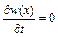 , то для стисливої рідини
, то для стисливої рідини 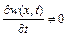 . При цьому якщо
. При цьому якщо 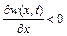 , то
, то 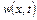 вздовж осі
вздовж осі  зменшується, тобто більше притікає рідини у даний об’єм, ніж із нього витікає, що призводить до зростання густини
зменшується, тобто більше притікає рідини у даний об’єм, ніж із нього витікає, що призводить до зростання густини 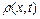 у часі, або ж
у часі, або ж 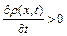 . Аналогічно, якщо
. Аналогічно, якщо 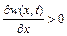 , то
, то 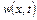 зростає вздовж осі
зростає вздовж осі  , тобто більше витікає рідини з даного об’єму, ніж у нього притікає, що призводить до зменшення густини
, тобто більше витікає рідини з даного об’єму, ніж у нього притікає, що призводить до зменшення густини 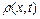 у часі, або
у часі, або 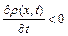 .
.
Проілюструємо сказане вище на прикладах. Позначимо через 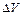 об’єм і припустимо, що
об’єм і припустимо, що 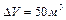 . Нехай кількість, що притікає за час
. Нехай кількість, що притікає за час 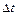 у цей об’єм, рідини буде
у цей об’єм, рідини буде 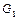 , а кількість рідини, що витікає,
, а кількість рідини, що витікає, 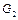 . Зміну маси у даному об’ємі за час
. Зміну маси у даному об’ємі за час 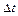 позначимо через
позначимо через 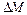 . Тоді
. Тоді
а) якщо 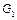 = 20 кг , a
= 20 кг , a 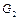 = 19 кг, тобто у зазначений об’єм більше притікає рідини, ніж випливає, то маса рідини збільшується на
= 19 кг, тобто у зазначений об’єм більше притікає рідини, ніж випливає, то маса рідини збільшується на
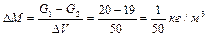 ,
,
тобто на 2%;
б) якщо 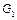 = 20 кг,, a
= 20 кг,, a 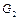 = 22 кг, тобто з цього об’єму більше випливає рідини, ніж у нього притікає, то маса рідини зменшується на
= 22 кг, тобто з цього об’єму більше випливає рідини, ніж у нього притікає, то маса рідини зменшується на
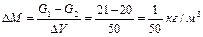 ,
,
тобто на 2%.
Тепер перейдемо до одержання математичного виразу закону сталості маси, тобто до виводу рівняння нерозривності стисливої рідини. Для одномірної течії рідини (рисунок 2.3) зміна кількості рідини 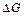 за деякий проміжок часу
за деякий проміжок часу 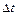 складе
складе
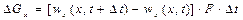 , (2.50)
, (2.50)
де 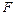 - площа поперечного перетину труби.
- площа поперечного перетину труби.
Зміна ж маси у аналізованому об’ємі 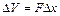 за той же проміжок часу
за той же проміжок часу
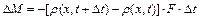 . (2.51)
. (2.51)
Як було зазначено вище, 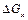 і
і 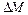 завжди будуть мати різні знаки. Прирівнюючи праві частини (2.25) і (2.26), одержуємо вираз закону сталості маси
завжди будуть мати різні знаки. Прирівнюючи праві частини (2.25) і (2.26), одержуємо вираз закону сталості маси
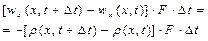 . (2.52)
. (2.52)
У результаті ділення останнього виразу на 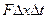 при переході до межі при
при переході до межі при 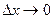 і
і 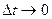 знаходимо
знаходимо
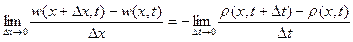 , (2.53)
, (2.53)
або ж
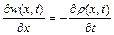 . (2.54)
. (2.54)
Рівняння (2.27) називається рівнянням нерозривності стисливої рідини при лінійному плині. Права частина, тобто 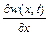 характеризує зміну густини рідини
характеризує зміну густини рідини 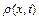 у часі, а ліва частина
у часі, а ліва частина 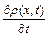 - зміну швидкості уздовж осі
- зміну швидкості уздовж осі  (осі труби).
(осі труби).
Тому 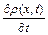 і
і 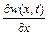 завжди будуть мати різні знаки. Рівняння (2.27) справедливо для будь-якої точки
завжди будуть мати різні знаки. Рівняння (2.27) справедливо для будь-якої точки  у будь-який момент часу
у будь-який момент часу 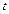 . Це пояснюється тим, що перерізи
. Це пояснюється тим, що перерізи  та
та 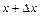 , а також моменти часу
, а також моменти часу 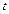 і
і 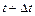 були узяті довільно, а для одержання (2.27) ми переходили до межі при
були узяті довільно, а для одержання (2.27) ми переходили до межі при 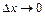 і
і 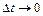 , тобто формула (2.27) була отримана для довільної точки
, тобто формула (2.27) була отримана для довільної точки  і довільного моменту часу
і довільного моменту часу 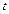 . Останнє зауваження ставиться також до випадку плоского і просторового плину рідини.
. Останнє зауваження ставиться також до випадку плоского і просторового плину рідини.
При плоскому плині рідини ми виходили з рисунка 2.4. Зміна кількості рідини за проміжок часу 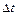 визначали за формулою
визначали за формулою
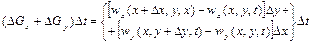 , (2.55)
, (2.55)
а зміну маси у аналізованому об’ємі - за формулою
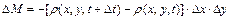 . (2.56)
. (2.56)
При виводі формул (2.28) і (2.29) розглядаємо паралелепіпед із шириною, рівною одиниці, довжиною 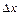 і висотою
і висотою  . Прирівнявши праві частини (2.28) і (2.29), попередньо розділивши їх на
. Прирівнявши праві частини (2.28) і (2.29), попередньо розділивши їх на 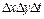 , і перейшовши до межі при
, і перейшовши до межі при 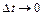 ;
; 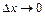 і
і 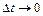 , одержимо
, одержимо
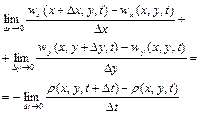 , (2.57)
, (2.57)
або
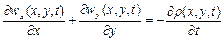 . (2.58)
. (2.58)
Це рівняння називається рівнянням нерозривності плоского плину стисливої рідини, і справедливо воно для будь-якої точки 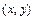 у будь-який момент часу
у будь-який момент часу 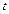 .
.
Нарешті, для одержання рівняння нерозривності при плині рідини у просторі ми виходили з рисунка 2.5. Зміну кількості рідини у аналізованому об’ємі 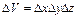 за проміжок часу
за проміжок часу 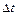 визначали за допомогою рівності
визначали за допомогою рівності
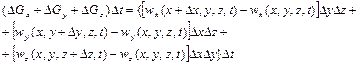 . (2.59)
. (2.59)
Зміна ж густини у аналізованому об’ємі 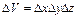 за аналізований проміжок часу
за аналізований проміжок часу 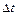 буде
буде
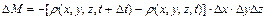 . (2.60)
. (2.60)
Прирівнявши праві частини (2.31) і (2.32), попередньо розділивши їх на 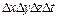 , і перейшовши до межі при
, і перейшовши до межі при 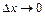 ;
;  ;
; 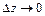 і
і 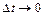 , одержимо
, одержимо
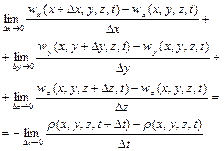 , (2.61)
, (2.61)
або
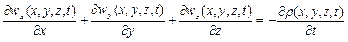 . (2.62)
. (2.62)
Це рівняння являє собою рівняння нерозривності при просторовій течії стисливої рідини. Права частина рівняння 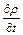 характеризує зміну густини у часі, а ліва - зміну кількості рідини у аналізованому об’ємі.
характеризує зміну густини у часі, а ліва - зміну кількості рідини у аналізованому об’ємі.
Рівняння (2.33) справедливо для будь-якої точки простору 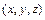 у будь-який момент часу
у будь-який момент часу 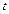 . Величини
. Величини 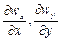 і
і 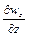 можуть мати як однакові, так і протилежні знаки. Проте у усіх випадках знаки
можуть мати як однакові, так і протилежні знаки. Проте у усіх випадках знаки 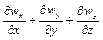 і
і 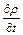 - будуть протилежними. Так, наприклад, якщо у точках зазначеного об’єму значення
- будуть протилежними. Так, наприклад, якщо у точках зазначеного об’єму значення 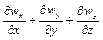 позитивне ( при цьому
позитивне ( при цьому 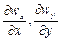 і
і 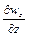 усі можуть бути позитивними або мати різні знаки), то це значить, що з зазначеного об’єму рідини випливає більше, ніж притікає. Останнє призводить до зменшення густини у цьому об’ємі у часі, тобто
усі можуть бути позитивними або мати різні знаки), то це значить, що з зазначеного об’єму рідини випливає більше, ніж притікає. Останнє призводить до зменшення густини у цьому об’ємі у часі, тобто 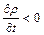 . Аналогічно, якщо значення
. Аналогічно, якщо значення 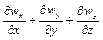 від¢ємне ( при цьому
від¢ємне ( при цьому 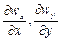 і
і 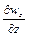 усі можуть бути від¢ємними або ж мати різні знаки), то у даний об’єм більше притікає рідини, чим випливає; останнє призводить до збільшення густини у часу у цьому об’ємі, і, отже,
усі можуть бути від¢ємними або ж мати різні знаки), то у даний об’єм більше притікає рідини, чим випливає; останнє призводить до збільшення густини у часу у цьому об’ємі, і, отже, 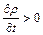 .
.
При одержанні рівняння нерозривності (2.33) підраховувалася зміна маси у об’ємі паралелепіпеда 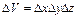 . Цей паралелепіпед заповнений. Якщо роздивитися фільтрацію рідини через однорідне пористе середовище шпаристістю т, то об’єм, зайнятий рідиною, стане рівним
. Цей паралелепіпед заповнений. Якщо роздивитися фільтрацію рідини через однорідне пористе середовище шпаристістю т, то об’єм, зайнятий рідиною, стане рівним 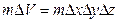 .
.
Тому рівняння нерозривності у цьому випадку буде
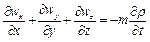 . (2.63)
. (2.63)
Аналогічно для плоского й одномірного плину з рівнянь (2.30) і (2.27) одержимо такі рівняння нерозривності плоскої й одномірної фільтрації рідини:
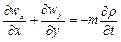 , (2.64)
, (2.64)
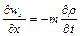 . (2.65).
. (2.65).
У випадку суміші рідин і газів, тобто перемінності складу уздовж об’єму, рівняння нерозривності виводиться для двокомпонентної системи. Склад суміші визначається масовою концентрацією c - відношенням маси даного компонента до загального маси рідини у заданому елементарному об’ємі.
Зміна відбувається шляхом механічного перемішування - склад об’єму , що рухається , не змінюється, але в кожній заданій нерухомій точці, що знаходиться в цьому місці рідини, c згодом буде змінюватися.
При дифузії під 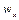 і
і 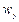 розуміються мольні швидкості потоку, а
розуміються мольні швидкості потоку, а 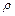 буде відповідати концентрації. Умовою дифузії є наявність градієнту концентрацій компонента , що дифундує, (аналогічно тому, як температурний градієнт є умовою теплопровідності). Будемо вважати, що маса, яка накопичується, викликає збільшення концентрації компонента
буде відповідати концентрації. Умовою дифузії є наявність градієнту концентрацій компонента , що дифундує, (аналогічно тому, як температурний градієнт є умовою теплопровідності). Будемо вважати, що маса, яка накопичується, викликає збільшення концентрації компонента 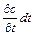 . За допомогою цього приросту концентрації також можна висловити масу , що накопичується в елементарному паралелепіпеді
. За допомогою цього приросту концентрації також можна висловити масу , що накопичується в елементарному паралелепіпеді 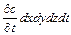 .
.
Закон збереження енергії.
Покажемо на прикладах, як можна застосовувати закон збереження енергії для опису деяких фізичних процесів.
У основному будуть розглядатися механічний і тепловий процеси, тому сформулюємо для них закон збереження енергії. Для механічних процесів сума кінетичної і потенційної енергії постійна.
При теплових процесах закон збереження енергії, або перший закон термодинаміки, записується так: нескінченно мала зміна внутрішньої енергії складається з двох частин - із кількості тепла, отриманого тілом, і виконаної тілом роботи.
Робота при надходженні тепла залежить від початкового і кінцевого стану тіла і від шляху, по якому змінюється стан тіла. Тому не можна розглядати тепловий ефект процесу як різницю цих кількостей у кінцевому і початковому станах.
З поглинанням тепла в кількості  температура підвищується на розмір
температура підвищується на розмір 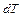 .
.
Відношення 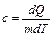 (де
(де 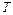 - маса тіла) називається теплоємністю тіла. У фізиці користуються теплоємністю при постійному тиску
- маса тіла) називається теплоємністю тіла. У фізиці користуються теплоємністю при постійному тиску 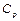 і теплоємністю при постійному об’ємі
і теплоємністю при постійному об’ємі 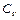 .
.
Застосуємо перший закон термодинаміки для дослідження процесу поширення тепла в тілі.
Розглядаються два перетини 2-2 і 2-2 (рисунок 2.7). Тіло має якусь визначену початкову температуру. До одного кінця тіла підводиться джерело тепла або холоду. Відповідно до цього в тілі відбувається нагрівання або охолодження.
Температура в якійсь точці тіла буде залежати від відстані точки до місця підводу тепла і часу 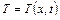 .
.
На поточний розподіл температури у тілі впливає початковий розподіл температури, а також умови у кінцевих перетинах тіл, зокрема від температури на обох кінцях тіла.
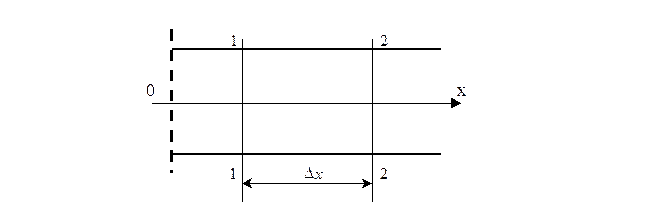
Рисунок 2.7 – Схема руху тепла.
У приведеному прикладі через перетин 2-2 у одиницю часу підводиться кількість тепла, рівна 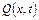 . Через перетин 2-2 у одиницю часу відводиться кількість тепла, рівне
. Через перетин 2-2 у одиницю часу відводиться кількість тепла, рівне 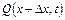 . Різниця між цими кількостями тепла
. Різниця між цими кількостями тепла
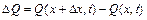 (2.66)
(2.66)
відповідно до першого закону термодинаміки витрачається на зміну температури у відсіку між перерізами 1-1 і 2-2.
Якщо 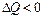 , то тіло нагрівається, у протилежному випадку – охолоджується , тобто у першому випадку
, то тіло нагрівається, у протилежному випадку – охолоджується , тобто у першому випадку
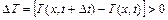 , (2.67)
, (2.67)
а у другому – 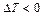 .
.
При зміні кількості підведеного й відведеного тепла на розмір 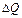 температура тіла (відповідно до закону збереження енергії і визначення теплоємності) повинна змінюватися на величину
температура тіла (відповідно до закону збереження енергії і визначення теплоємності) повинна змінюватися на величину
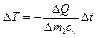 ; (2.68)
; (2.68)
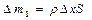 , (2.69)
, (2.69)
де 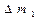 - елементарна маса тіла;
- елементарна маса тіла; 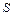 - площа поперечного перетину тіла;
- площа поперечного перетину тіла; 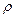 - густина тіла.
- густина тіла.
Так як 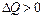 при
при 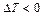 і
і 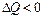 при
при 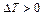 , у правій частині (2.68) поставлений знак мінус.
, у правій частині (2.68) поставлений знак мінус.
Підставивши у (2.68) значення 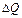 і
і 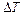 відповідно з (2.60), (2.62) і розділивши його на
відповідно з (2.60), (2.62) і розділивши його на 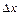 і
і 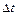 при
при 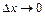 і
і 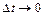 , одержимо
, одержимо
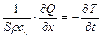 . (2.70)
. (2.70)
Таким чином, в одному рівнянні одержуємо два невідомих 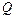 і
і 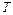 . Покажемо застосування закону збереження механічної енергії.
. Покажемо застосування закону збереження механічної енергії.
Позначимо через 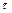 - дотичну напругу. Виведемо диференційне рівняння прямування у круглій циліндричній трубі уздовж кільця. Для цього виділимо у зоні на відстані
- дотичну напругу. Виведемо диференційне рівняння прямування у круглій циліндричній трубі уздовж кільця. Для цього виділимо у зоні на відстані 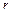 від осі труби елементарний кільцевий прошарок товщиною
від осі труби елементарний кільцевий прошарок товщиною 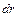 та довжиною
та довжиною 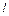 і складемо рівняння рівноваги сил, що діють на виділений елемент. Цими силами будуть: гальмівна сила
і складемо рівняння рівноваги сил, що діють на виділений елемент. Цими силами будуть: гальмівна сила 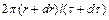 , сила прискорення
, сила прискорення 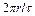 , сила тиску
, сила тиску 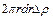 і сила енергії
і сила енергії 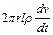 .
.
За принципом д'Аламбера, сума цих сил повинна дорівнювати нулю. Якщо при цьому врахувати, що перша й остання з цих сил діють у напрямку, оберненому дії інших двох сил, то
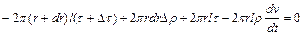 . (2.71)
. (2.71)
Зневажаючи розміром 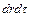 у порівнянні з іншими членами, одержуємо
у порівнянні з іншими членами, одержуємо
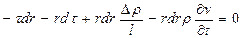 . (2.72)
. (2.72)
Дата добавления: 2015-10-09; просмотров: 1080;
