Основні поняття. Через u позначимо швидкість руху частинки
Через u позначимо швидкість руху частинки. Причому, якщо рух усталений, то 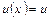 , де
, де 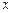 – віддаль від точки, яка рухається, до деякого початку
– віддаль від точки, яка рухається, до деякого початку 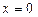 . При такому записі задається залежність (функціональна) швидкості точки, що рухається, від її положення, тобто від значення місцезнаходження частинки ( її віддалі від початку відліку
. При такому записі задається залежність (функціональна) швидкості точки, що рухається, від її положення, тобто від значення місцезнаходження частинки ( її віддалі від початку відліку 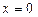 ). За допомогою
). За допомогою 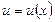 можемо визначити її швидкість. Так, наприклад, при вільному падінні частинки масою
можемо визначити її швидкість. Так, наприклад, при вільному падінні частинки масою 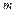 з висоти
з висоти 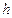 в середовищі, опором якого нехтуємо, швидкість частинки в залежності від її положення визначається формулою
в середовищі, опором якого нехтуємо, швидкість частинки в залежності від її положення визначається формулою
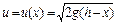 , (2.1)
, (2.1)
де 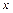 – віддаль частинки від поверхні землі (від початку відліку
– віддаль частинки від поверхні землі (від початку відліку 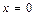 ).
).
Надаючи різних значень 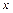 , у формулі (2.1) можна знайти швидкість частинки, яка падає, на різних віддалях від поверхні землі. При визначенні швидкості частинки в різних її положеннях (її віддалях від поверхні землі)
, у формулі (2.1) можна знайти швидкість частинки, яка падає, на різних віддалях від поверхні землі. При визначенні швидкості частинки в різних її положеннях (її віддалях від поверхні землі) 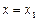 ;
; 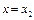 та ін. досить у формулі (2.1) замінити
та ін. досить у формулі (2.1) замінити 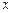 на
на 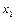 ,
, 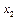 та ін. Якщо, наприклад,
та ін. Якщо, наприклад, 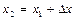 , то за формулою (2.2)
, то за формулою (2.2) 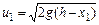 - швидкість частинки у положенні
- швидкість частинки у положенні 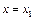 , а
, а 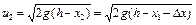 - швидкість частинки у положенні
- швидкість частинки у положенні 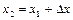 (рисунок 2.1).
(рисунок 2.1).
Таким чином, 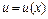 або
або 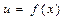 визначає швидкість частинки, яка знаходиться на віддалі
визначає швидкість частинки, яка знаходиться на віддалі 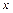 від початку відліку. Точно також
від початку відліку. Точно також 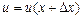 визначає швидкість тієї ж частинки на віддалі
визначає швидкість тієї ж частинки на віддалі 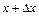 від початку відліку. Зміна швидкості частинки при переході з положення
від початку відліку. Зміна швидкості частинки при переході з положення 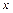 в положення
в положення 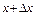 визначається рівністю
визначається рівністю
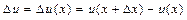 . (2.2)
. (2.2)
В подальшому 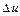 будемо називати приростом функції, а
будемо називати приростом функції, а 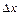 – приростом аргументу. При цьому малим значенням
– приростом аргументу. При цьому малим значенням 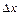 відповідають малі значення
відповідають малі значення 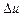 . Іншими словами, якщо
. Іншими словами, якщо 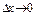 , то
, то 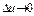 .
.
Необхідно зауважити, що 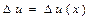 також є функцією
також є функцією 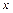 , тобто при одному і тому ж прирості
, тобто при одному і тому ж прирості 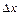 приріст функції для різних точок
приріст функції для різних точок 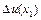 і
і 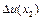 не буде рівним.
не буде рівним.
Так як в подальшому приймемо 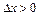 , то зупинимося на визначенні знаку приросту функції
, то зупинимося на визначенні знаку приросту функції 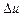 .
.
Якщо 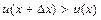 , тобто, наприклад, швидкість в точці
, тобто, наприклад, швидкість в точці 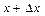 більше, ніж в точці
більше, ніж в точці 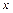 , то
, то 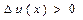 і швидкість точки зростає. Якщо ж
і швидкість точки зростає. Якщо ж 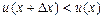 , тобто значення функції (в нашому прикладі значення швидкості) в точці
, тобто значення функції (в нашому прикладі значення швидкості) в точці 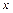 більше, ніж в точці
більше, ніж в точці 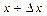 , то
, то 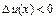 , і функція, що розглядається, спадає.
, і функція, що розглядається, спадає.
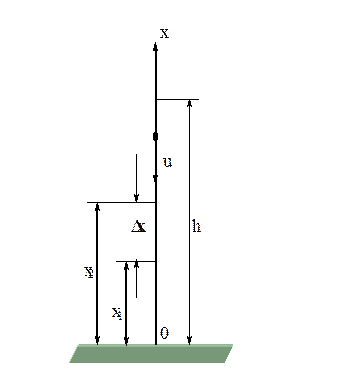
Рисунок 2.1 – Рух частинки при падінні.
Таким чином, у всьому інтервалі, де 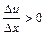 , функція
, функція 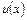 росте, а де
росте, а де 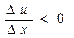 - вона спадає. На рисунку 2.2 в інтервалі
- вона спадає. На рисунку 2.2 в інтервалі 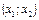 функція
функція 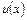 зростає, і, отже, в усіх точках цього інтервалу
зростає, і, отже, в усіх точках цього інтервалу 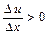 , а в інтервалі
, а в інтервалі 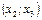 вона спадає і, отже,
вона спадає і, отже, 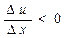 .
.
Відношення 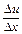 характеризує швидкість зміни функції в залежності від
характеризує швидкість зміни функції в залежності від 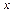 на відрізку
на відрізку 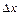 . Щоб знайти характер зміни
. Щоб знайти характер зміни 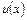 в даній точці
в даній точці  , необхідно обчислити
, необхідно обчислити
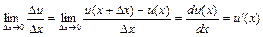 . (2.2)
. (2.2)
Формула (2.2) характеризує швидкість зміни 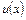 у залежності від
у залежності від  . Вона дає похідну від функції
. Вона дає похідну від функції 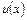 по аргументу
по аргументу  . Якщо функція
. Якщо функція 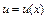 є залежністю швидкості від положення рухомої точки, то
є залежністю швидкості від положення рухомої точки, то 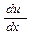 дає значення градієнта швидкості
дає значення градієнта швидкості 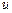 у напрямі осі
у напрямі осі  , тобто характеризує швидкість (і характер) зміни швидкості. Якщо
, тобто характеризує швидкість (і характер) зміни швидкості. Якщо 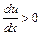 , то швидкість
, то швидкість 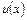 на шляху
на шляху  зростає, якщо ж
зростає, якщо ж 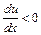 , то вона зменшується.
, то вона зменшується.
Чим більша абсолютна величина 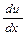 , тим більша зміна швидкості в точці
, тим більша зміна швидкості в точці  . Таким чином, якщо на деякому інтервалі
. Таким чином, якщо на деякому інтервалі 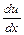 додатна величина, то це означає зростання функції
додатна величина, то це означає зростання функції 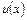 , а якщо від'ємна велиична, то – зменшення. Якщо ж в деякій точці
, а якщо від'ємна велиична, то – зменшення. Якщо ж в деякій точці 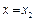 має місце
має місце 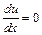 , то в цій точці функція
, то в цій точці функція 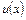 досягає або свого максимуму (точка переходу від зростання до зменшення), або свого мінімуму (точка переходу від зменшення до зростання).
досягає або свого максимуму (точка переходу від зростання до зменшення), або свого мінімуму (точка переходу від зменшення до зростання).
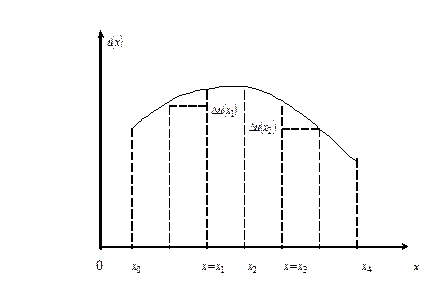 Рисунок 2.2 – Характер зміни функції.
Рисунок 2.2 – Характер зміни функції.
При неусталеному русі, коли швидкість частинки, що рухається, не тільки змінюється при переході з одної точки до іншої, але і у кожній точці змінюється у часі, позначимо через 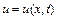 швидкість точки, яка знаходиться на віддалі
швидкість точки, яка знаходиться на віддалі  від початку відліку у момент часу
від початку відліку у момент часу 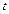 . Точно також через
. Точно також через 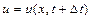 позначимо швидкість тієї ж частинки у момент часу
позначимо швидкість тієї ж частинки у момент часу 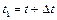 . Таким чином,
. Таким чином, 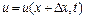 буде означати швидкість точки, яка знаходиться на віддалі
буде означати швидкість точки, яка знаходиться на віддалі 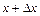 від початку відліку у момент часу
від початку відліку у момент часу 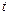 , і, нарешті,
, і, нарешті, 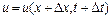 - швидкість частинки у точці
- швидкість частинки у точці 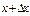 у момент часу
у момент часу 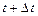 .
.
Необхідно особливо зауважити, що, у загальному випадку, 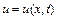 ,
, 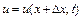 ,
, 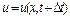 і
і 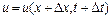 між собою не рівні, але усі вони будуть прямувати до величини
між собою не рівні, але усі вони будуть прямувати до величини 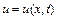 при
при 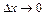 і
і 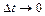 . У нашому прикладі
. У нашому прикладі 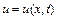 і
і 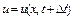 відповідають значенням швидкості частинки на віддалі
відповідають значенням швидкості частинки на віддалі  від початку відліку у моменти часу
від початку відліку у моменти часу 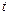 і
і 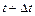 . Тому
. Тому 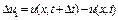 є приростом швидкості частинки в даній точці
є приростом швидкості частинки в даній точці  за проміжок часу
за проміжок часу 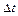 . Точно також
. Точно також 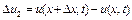 є різниця швидкостей частинок, які характеризуються у точках х і
є різниця швидкостей частинок, які характеризуються у точках х і 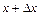 у момент часу
у момент часу 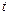 . Іншими словами,
. Іншими словами, 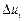 характеризує зміну швидкості у часі в даній фіксованій точці
характеризує зміну швидкості у часі в даній фіксованій точці  , а
, а 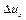 - зміну швидкості у даний момент часу
- зміну швидкості у даний момент часу 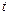 у різних точках
у різних точках  і
і 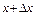 . При цьому
. При цьому 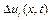 і
і 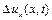 будуть залежати від
будуть залежати від  і
і 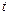 .
.
Якщо 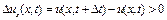 , то у даній точці
, то у даній точці  швидкість частинки з часом росте, якщо ж
швидкість частинки з часом росте, якщо ж 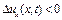 , то вона зменшується.
, то вона зменшується.
Аналогічно 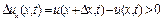 , то швидкість у точці
, то швидкість у точці 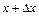 у даний момент часу
у даний момент часу 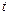 більше, ніж в точці
більше, ніж в точці  , якщо ж
, якщо ж 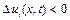 , то швидкість у точці
, то швидкість у точці  більше, ніж у точці
більше, ніж у точці 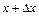 . Відзначимо, що і в цьому випадку при
. Відзначимо, що і в цьому випадку при 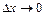 величина
величина 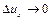 і при
і при 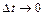 величина
величина 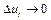 .
.
Характер зміни 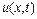 у різних точках
у різних точках  у даний момент часу
у даний момент часу 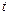 можна виразити формулою
можна виразити формулою
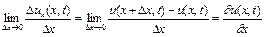 . (2.3)
. (2.3)
Ця рівність являє собою часткову похідну від функції 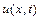 по
по  у даний момент часу
у даний момент часу 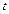 , яка характеризує поведінку функції ( її зростання чи зменшення, а також швидкість зміни ) вздовж осі
, яка характеризує поведінку функції ( її зростання чи зменшення, а також швидкість зміни ) вздовж осі  в даний момент часу
в даний момент часу 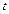 .
.
Також
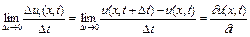 , (2.4)
, (2.4)
є частковою похідною від функції 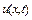 за часом
за часом 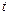 у фіксованій точці
у фіксованій точці  , яка характеризує поведінку функції ( її зростання чи зменшення, а також швидкість зміни у часі в розглядуваній точці
, яка характеризує поведінку функції ( її зростання чи зменшення, а також швидкість зміни у часі в розглядуваній точці  ).
).
Таким чином, якщо 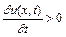 , то в усіх розглядуваних точках функція
, то в усіх розглядуваних точках функція 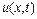 росте у часі, якщо ж
росте у часі, якщо ж 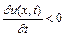 , то – спадає. Також, якщо
, то – спадає. Також, якщо 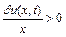 , то в даний момент часу
, то в даний момент часу 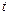 вздовж осі
вздовж осі  функція
функція 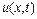 росте, а при
росте, а при 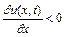 , спадає.
, спадає.
Ще раз зауважимо, що за допомогою формули (2.2) визначається зміна швидкості (функція 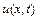 вздовж осі
вздовж осі  у даний фіксований момент часу
у даний фіксований момент часу 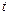 ), а за допомогою формули (2.4) – зміна швидкості (функція
), а за допомогою формули (2.4) – зміна швидкості (функція 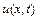 в часі у даній фіксованій точці
в часі у даній фіксованій точці  ). Іншими словами, при одержанні формули (2.3) час
). Іншими словами, при одержанні формули (2.3) час 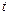 рахуємо фіксованим, а при одержанні формули (2.4) значення
рахуємо фіксованим, а при одержанні формули (2.4) значення  рахується фіксованим. Тому
рахується фіксованим. Тому
 (2.5)
(2.5)
означає зміну швидкості (функція 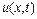 ) уздовж осі
) уздовж осі  у даний момент часу
у даний момент часу 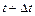 . Причому при
. Причому при 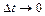 формули (2.3) і (2.5) співпадають. Також
формули (2.3) і (2.5) співпадають. Також
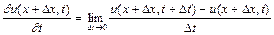 (2.6)
(2.6)
означає зміну швидкості (функція 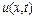 в часі у даній фіксованій точці
в часі у даній фіксованій точці 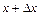 . Причому при
. Причому при 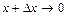 формули (2.4) і (2.6) співпадають.
формули (2.4) і (2.6) співпадають.
З математичного аналізу відомо, що, якщо
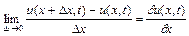 , (2.7)
, (2.7)
то
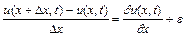 , (2.8)
, (2.8)
де 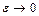 при
при 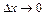 , тобто при малих значеннях
, тобто при малих значеннях 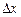 величина
величина 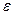 як завгодно мала.
як завгодно мала.
Перепишемо (2.8) у вигляді
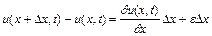 . (2.9)
. (2.9)
Так як 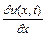 - величина кінцева і не залежить від
- величина кінцева і не залежить від 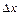 , то при малих значеннях
, то при малих значеннях 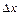 другий член у правій частині формули (2.9), тобто
другий член у правій частині формули (2.9), тобто 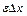 , є мала величина більш високого порядку, ніж перший член
, є мала величина більш високого порядку, ніж перший член 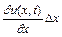 . Тому, нехтуючи величиною
. Тому, нехтуючи величиною 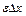 у порівнянні з
у порівнянні з 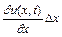 і позначаючи
і позначаючи 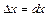 для значень
для значень 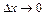 , з формули (2.9) одержимо
, з формули (2.9) одержимо
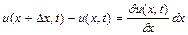 . (2.10)
. (2.10)
Таким же чином з формули (2.7) знаходимо
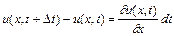 . (2.11)
. (2.11)
Нижче наведемо деякі відомості з векторного числення, необхідні при подальшому поданні матеріалу.
Векторна величина а визначається в загальному випадку трьома проекціями на осі декартової системи координат, тобто
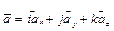 , (2.12)
, (2.12)
де 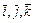 - одиничні вектори відповідно осей
- одиничні вектори відповідно осей 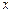 ,
, 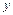 і
і 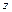 .
.
Величину 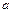 знаходимо за формулою
знаходимо за формулою
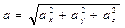 . (2.13)
. (2.13)
Градієнт скалярної величини 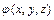 (grad) є вектором, направленим по нормалі до поверхні
(grad) є вектором, направленим по нормалі до поверхні 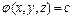 . Наприклад, в випадку плоско-радіальної фільтрації нестискуваної рідини (одиночна циліндрична свердловина в центрі круглого циліндричного пласта ) градієнт тиску направлений по радіусу, так як поверхні рівного тиску – циліндричні кола. Градієнт скалярної величини виражається формулою
. Наприклад, в випадку плоско-радіальної фільтрації нестискуваної рідини (одиночна циліндрична свердловина в центрі круглого циліндричного пласта ) градієнт тиску направлений по радіусу, так як поверхні рівного тиску – циліндричні кола. Градієнт скалярної величини виражається формулою
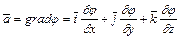 , (2.14)
, (2.14)
де 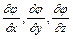 - проекції вектора
- проекції вектора 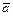 відповідно на осі
відповідно на осі  ,
, 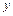 і
і 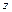 , отже
, отже
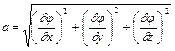 . (2.15)
. (2.15)
Широко застосовується в нафтопромисловій механіці і поняття скалярної величини – дивергенції векторної величини 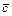
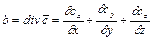 , (2.16)
, (2.16)
де 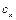 ,
, 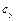 i
i 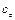 – проекції на осі
– проекції на осі  ,
, 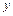 і
і 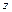 .
.
Виходячи з визначення дивергенції і градієнта маємо
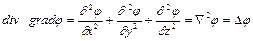 . (2.17)
. (2.17)
Знак 
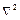 (набла в квадраті), або
(набла в квадраті), або 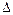 (дельта), носить назву оператора Лапласа.
(дельта), носить назву оператора Лапласа.
Дата добавления: 2015-10-09; просмотров: 948;
