Схема вычисления производной

Схема нахождения производной функции у = f(х) включает следующие этапы:

1. Дают аргументу х приращение Dх ¹ 0 и находят значение функции
у = f(х + Dх).

2. Находят приращение функции Dу = f(х + Dх) - f(х).

3. Составляют отношение Dу/Dх.

4. Находят его предел при Dх ® 0 (если этот предел существует).

Рассмотрим эти этапы на примере функции у = х³. Чтобы найти ее производную, дадим аргументу приращение Dх ¹ 0 и найдем у = f(х + Dх) =
= (х + Dх)³ = х³ + 3х²Dх + 3хDх² + Dх³. Затем найдем приращение функции
Dу = f(х + Dх) - f(х) = f(х + Dх) - х³ = 3х²Dх + 3хDх² + Dх³ = Dх (3х² + 3хDх +
+ Dх²). Составим отношение Dу/Dх = 3х² + 3хDх + Dх². Найдем его предел .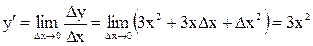

Можно доказать, что для любого n (xⁿ)` = nx^n-1.