Основные правила дифференцирования
Рассмотрим их без доказательства.
1. Производная постоянной равна нулю, т.е. с' = 0 (это очевидно, так как любое приращение постоянной функции равно нулю).
2. Производная аргумента равна 1, т.е. х` = 1 (правило следует из формулы для производной степенной функции).
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций:
(u + v)' = u' + v'.
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: (uv)'=u'v + v'u.
Следствие 1. Постоянный множитель можно выносить за знак производной: (сu)' = сu'.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: (uvw)' = u'vw + uv'w + + uvw'.
5. Производная частного двух дифференцируемых функций может быть найдена по формуле 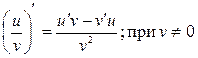 .
.
6. Если у = f(u) и u = j(х) - дифференцируемые функции от своих аргументов, то производная сложной функции у = f([j(х)]) существует и равна производной данной функции по промежуточному аргументу u, умноженной на производную самого промежуточного аргумента по независимой переменной х: y` = f `(u)*u`.
7. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции: 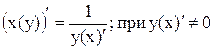 .
.
Проиллюстрируем последнее правило на примере взаимно обратных функций, производные которых мы уже знаем. Возьмем степенную функцию y = x3, y` = 3x2. Такую же производную можно получить, если воспользоваться обратной функцией. В самом деле, 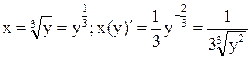 . По правилу
. По правилу 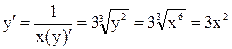 .
.
Дата добавления: 2015-10-06; просмотров: 705;
