Дифференцируемость функции

Нахождение производной функции называется ее дифференцированием.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке.

Теорема о зависимости между непрерывностью и днфференцируемостью функции: если функция дифференцируема в точке, то она в этой точке непрерывна.

Без доказательства.

Замечание: обратное утверждение в общем случае не является верным, т.е. если функция непрерывна в данной точке, то она не обязательно в ней дифференцируема. Непрерывность функции является необходимым, но не достаточным условием ее дифференцируемости.

Приведем пример функции, которая, являясь непрерывной в точке
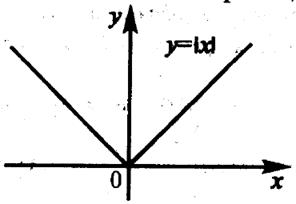
х = 0, при этом недифференцируема в этой точке. На рисунке 3.2 представлен график функции у = |х|. Она непрерывна в точке
х = 0. Производная функция (если она существует) равна 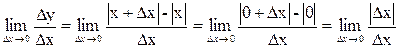. Последний предел не существует, так как односторонние пределы в этой точке не совпадают ( 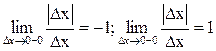). Следовательно, производная в точке х = 0 не существует (геометрически это означает отсутствие касательной к кривой в точке х = 0).