Физический и экономический смысл производной
Рассмотрим прямолинейное движение по закону s=s(t), где s - пройденный путь, а t – время. Необходимо найти скорость движения v в момент t0.
За промежуток времени Dt с момента t0 будет пройдено расстояние
Ds = s(t0 + Dt) - s(t0). Тогда средняя скорость за этот промежуток времени составит Ds/Dt. Чем меньше будет промежуток Dt, тем лучше это отношение будет оценивать скорость в момент времени t0: 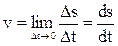 .
.
Таким образом, производная функции представляет собой скорость изменения значения функции в точке. Этот смысл производной удобно использовать не только в физике, но и в экономике.
Например, если функция p = p(q) выражает зависимость прибыли p от объема произведенной продукции q, то ее производная показывает предельный рост прибыли (скорость изменения прибыли при изменении объема производства): 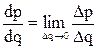 . Если функция q = q(u) выражает зависимость объема производства q от числа работников u, то ее производная показывает скорость изменения этого объема при изменении числа работников:
. Если функция q = q(u) выражает зависимость объема производства q от числа работников u, то ее производная показывает скорость изменения этого объема при изменении числа работников: 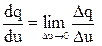 (предельная производительность дополнительного работника). Если функция описывает зависимость объема производства от времени, то получим производительность в единицу времени. Если функция w = w(q) выражает зависимость издержек производства от количества выпускаемой продукции, то ее производная означает предельные издержки (приближенно показывает дополнительные затраты на производство единицы дополнительной продукции):
(предельная производительность дополнительного работника). Если функция описывает зависимость объема производства от времени, то получим производительность в единицу времени. Если функция w = w(q) выражает зависимость издержек производства от количества выпускаемой продукции, то ее производная означает предельные издержки (приближенно показывает дополнительные затраты на производство единицы дополнительной продукции): 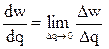 И т.п.
И т.п.
На основе понятия производной в экономике рассчитываются предельная выручка, предельный доход, предельный продукт, предельная полезность, предельная производительность и другие предельные величины.
Предельные величины характеризуют процесс изменения экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) во времени или относительного другого исследуемого фактора.
Дата добавления: 2015-10-06; просмотров: 1057;
