В выражении производной по направлению
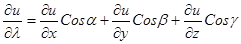
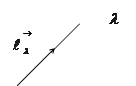 множители
множители 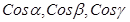 можно рассматри
можно рассматри
вать как проекции на координатные оси
единичного вектора луча 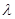
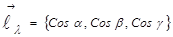
рассмотрим вектор, проекции которого на
координатные оси равны значениям частных производных
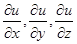 в выбранной точке P(x,y,z). Этот вектор носит особое название – градиент функции
в выбранной точке P(x,y,z). Этот вектор носит особое название – градиент функции 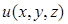 . Обозначают его одним из символов: grad uили
. Обозначают его одним из символов: grad uили 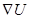 . Значок
. Значок 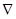 называется оператором «Набла », читается «Набла u».Введён английским математиком Гамильтоном.
называется оператором «Набла », читается «Набла u».Введён английским математиком Гамильтоном.
Определение:Градиентом функции u(x,y,z) называется вектор, проекциями которого служат значения частных производных этой
Функции, т.е. 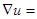 grad u
grad u 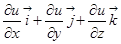 .
.
Из определения видно, что проекции графика на координатные оси зависят от точки P(x,y,z) и изменяются с изменением её координат. Тем самым каждоё точке из области определения функции u(x,y,z) соответствует определённый вектор – градиент этой функции. Из определения градиента и выражения производной по направлению 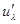 видно, что
видно, что 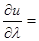 grad u
grad u 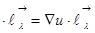 , т.е. производная функции по направлению равна скалярному произведению градиента функции на единичный вектор направления. Но grad u
, т.е. производная функции по направлению равна скалярному произведению градиента функции на единичный вектор направления. Но grad u 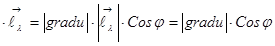
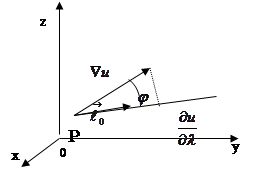
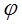 - угол между градиентом и лучом
- угол между градиентом и лучом 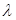 ,
,
но тогда 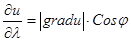 , т.е. производная функции по направлению равна проекции y градиента функции на направление дифференцирования. Отсюда видно, что наибольшее значение производная достигает, когда
, т.е. производная функции по направлению равна проекции y градиента функции на направление дифференцирования. Отсюда видно, что наибольшее значение производная достигает, когда 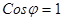 ,т.е.
,т.е. 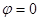 . И равно это наибольшее значение
. И равно это наибольшее значение 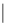 grad u
grad u  .Таким образом,
.Таким образом, 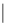 grad u
grad u 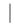 иесть наибольшее возможное значение производной
иесть наибольшее возможное значение производной 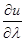 в данной точке P, а направление grad u совпадает с направлением луча из точки P, вдоль которого функция и меняется быстрее всего, т.е. направление градиента есть направление быстрейшего изменения функции u(x,y,z). Между градиентом и поверхностями уровня функции есть определённая связь.
в данной точке P, а направление grad u совпадает с направлением луча из точки P, вдоль которого функция и меняется быстрее всего, т.е. направление градиента есть направление быстрейшего изменения функции u(x,y,z). Между градиентом и поверхностями уровня функции есть определённая связь.
Теорема:Направление градиента функции u(x,y,z) в каждой точке совпадает с направлением нормали к поверхности уровня этой функции, проходящей через эту точку.
Доказательство. Возьмём любую точку из области определения функции 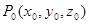 . Уравнение поверхности уровня, проходящей через точку
. Уравнение поверхности уровня, проходящей через точку 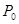 будет
будет
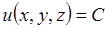
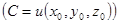
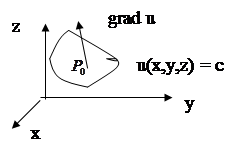 Уравнение нормали к этой поверхности в точке
Уравнение нормали к этой поверхности в точке 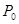 будет
будет
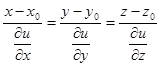 ,
,
т.е. координаты направляющего вектора нормали 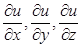 . Но это и значит, что grad u является таким вектором (у него такие же координаты).
. Но это и значит, что grad u является таким вектором (у него такие же координаты).
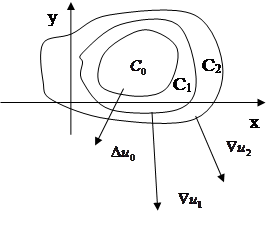 Замечание:в случае плоскости для функции
Замечание:в случае плоскости для функции 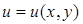 поверхности уровня есть линии уровня и grad u лежит в плоскости XOY. По теореме grad u в каждой точке перпендикулярен линии уровня, проходящей через эту точку. Проводя линии уровня и отмечая в различных точках вектор
поверхности уровня есть линии уровня и grad u лежит в плоскости XOY. По теореме grad u в каждой точке перпендикулярен линии уровня, проходящей через эту точку. Проводя линии уровня и отмечая в различных точках вектор 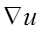 , мы получим графическое изображение поля, определяемого функцеий
, мы получим графическое изображение поля, определяемого функцеий 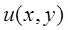 . В том направлении, где линии уровня расположены гуще, поля изменяютя быстрее. А grad u показывает величину и точное направление наибыстрейшего изменения.
. В том направлении, где линии уровня расположены гуще, поля изменяютя быстрее. А grad u показывает величину и точное направление наибыстрейшего изменения.
Основные свойства градиента функции ( 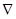 - оператора).
- оператора).
1. 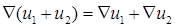 ;
;
2. 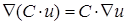 ;
;
3. 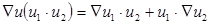
доказательство этих свойств аналогичные. Докажем 3.
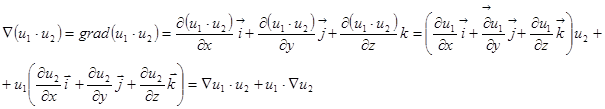
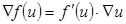 или
или 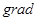
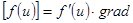 u – градиент сложной функции равен производной функции по промежуточному аргументу, умноженный на его градиент. Действительно
u – градиент сложной функции равен производной функции по промежуточному аргументу, умноженный на его градиент. Действительно 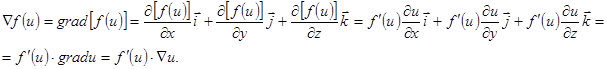 Эти свойства показывают, что свойства градиента похожи на свойства производных функций.
Эти свойства показывают, что свойства градиента похожи на свойства производных функций.
Пример: С какой наибольшей скоростью может возрастать функция 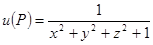 при переходе точки
при переходе точки 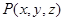 через
через 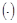
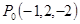 ?
?
Решение. Согласно теории наибольшая скорость возрастания функции в 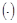
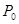
будет в направлении градиента и величина скорости равна модулю градиента в этой точке.
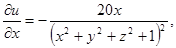
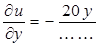 ,
, 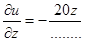
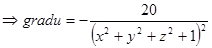
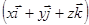
grad u 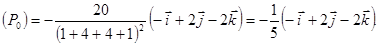 .
.
Построив вектор, реально получим направление наибольшего возрастания функции, его величина в точке 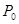 будет
будет 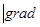 u
u 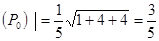 .
.
§12 ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Понятие экстремума ф. н. п. вводится также, как и для функции одной переменной.
Дата добавления: 2015-10-05; просмотров: 1085;
