Ограничимся случаем функции двух переменных.

Определение:Говорят ,что функция 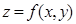имеет максимум(минимум) в точке M 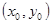, т.е. при 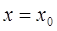, , 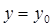если для всех точек 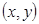достаточно близких к точке 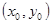и отличных от неё выполняется неравенство .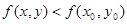

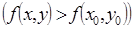В случае большего числа переменных определяется аналогично.

Точка 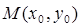называется точкой максимума(минимума) или экстремума, а значение - экстремальным .

Выясним условие существования экстремума ф. н. п. которые позволяют их отыскивать.

Теорема 1:Если функция достигает экстремума в точке 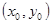, то каждая её частная производная первого порядка в этой точке или обращается в нуль или не существует.

Доказательство. Пусть функция имеет в точке 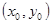экстремум. Для определённости, например max. Тогда вблизи точки 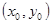выполняется неравенство Зафиксируем значение y, взяв его равным 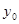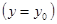. Тогда получим функцию одного переменного 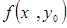, которая для значений x, близких к 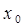удовлетворяет неравенству т.е она имеет max в точке 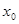. Но тогда её производная 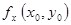в точке 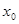либо =0, либо не существует. Но эта производная есть частная производная функции 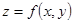: . Совершенно аналогично доказывается , что и 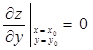или не существует. В случае большего числа переменных теорема аналогична. Теорема 1 даёт лишь необходимые условия существования экстремума, достаточными они не являются.

Например: функция в точке (0,0) имеет частные производные 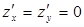. Но экстремума она в 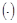(0,0) не имеет. В точке(0,0) z = 0. Однако, вблизи точки она принимает и + и – значения . и не достигает 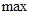ни ни 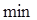. График поверхности есть гиперболический параболоид. Он в окрестности точки (0,0) имеет вид седла.

Точки, в которых частные производные функции равны нулю или не существуют(конечные) называются критическими точкамиили подозрительными наэкстремум. Теорема 1 утверждает, что экстремум может быть ( если он вообще есть) только в критических точках. Но он может в некоторых, а может быть и во всех критических точках, тоже не существовать. Исследование критических точек в случае функции двух переменных позволяет теорема.

Теорема 2: ( достаточные условия существования экстремума)

Если в некоторой окрестности критической точки 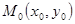функция 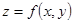определена, непрерывна и имеет непрерывные частные производные 1 и 2 порядков включительно, а в самой точке 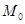выполняется условие

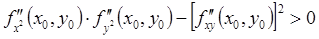, то функция 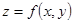имеет в точке 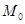экстремум: min, если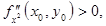

max, если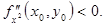

В случае 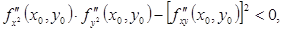экстремума в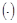 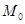нет. В случае равенства нулю этого выражения ничего определённого сказать нельзя (нужны дополнительные исследования).

Сразу заметим, что теорема 2 применима лишь к стационарным критическимточкам, т.е. где 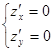В других , вообще, нет смысла говорить о вторых частных производных.

Условия теоремы часто пишут короче: .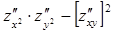

Пример 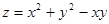. Д – вся плоскость 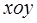. Найти экстремум функции.

Решение , , .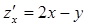

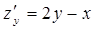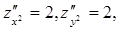
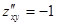Из условий 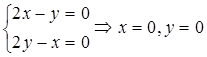единственная критическая точка (других нет), к тому же – стационарная. , , .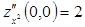

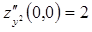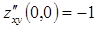Применим достаточное условие: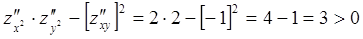

экстремум в точке (0,0) есть. Так как .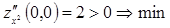

Итак в точке O(0,0) функция имеет min.

Заметим, что для данной функции можно было бы сразу сказать, что в точке (0,0) она имеет min: 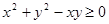. Но это лишь подтверждает эффективность теоремы и , к тому же, полностью решает вопрос о наличии экстремумов. Из решения ясно, что экстремум только один: min в точке (0,0) , z(0,0)=0.

§13 Наибольшее и наименьшее значение функции.

Пусть функция z = f(x,y) определена в некоторой замкнутой области D (т.е. в области с границей ). Требуется найти наибольшее и наименьшее значения функции в этой области. Если какое-либо из этих значений достигается внутри области, то это есть, очевидно, экстремальное значение. Но наибольшее и наименьшее значения могут достигаться и в точках границы. Отсюда следует правило: чтобы найти наибольшее (наименьшее) значение функции в замкнутой области, нужно найти все внутренние критические точки, вычислить значения функции в них и сравнить эти значения с наибольшими ( наименьшими) значениями функции в этой области.

Пример. Найти наибольшее и наименьшее значение функции 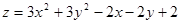в замкнутом треугольнике с вершинами O(0,0) , A(0,1) и B(1,0)

Решение:

1.Ищем критические точки внутри OAB.

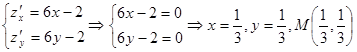- критическая точка внутри

.

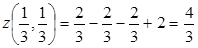2. Ищем наибольшие и наименьшие значения на границе. Рассматриваем отдельные отрезки.

1)На OA: 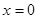, 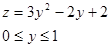- функция одной переменной y на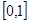

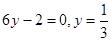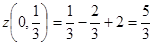, , . Вычислим значения на концах : 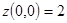, 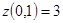. 2) На OB: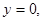 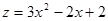- функция одной

переменной x на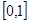

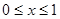
Аналогично: ,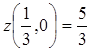

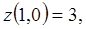
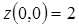
На AB: 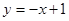, 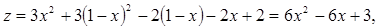Опять имеем функцию одной переменной на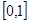 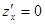при 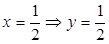, 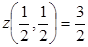. В точках A и B значения уже вычислялись: .

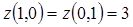Итак, наибольшее значение z =3 достигается в точках A и B , наименьшее значение 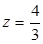достигается в точке .

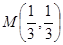§ 14.УСЛОВНЫЙ ЭКСТРЕМУМ. МЕТОД МНОЖИТЕЛЕЙ ЛАНГРАЖА.

Часто в задачах приходится отыскивать экстремумы функции от нескольких переменных, которые не являются независимыми, а связаны некоторым (или некоторыми) условиями – например, должны удовлетворять одному или нескольким уравнениям (уравнениям связи).

Пример. Нужно изготовить коробку в форме параллелепипеда наибольшего объёма при заданной площади поверхности 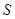коробки (площадь имеющегося материала).

Математически задача звучит так. Если 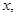z – длина, ширина, высота коробки, то , .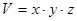

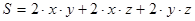Нужно найти максимум функции 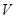при дополнительном условии, т.е. это типичная задача на условный экстремум.

Как решать такие задачи? Рассмотрим сначала вопрос в общем виде.

I. Пусть 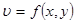(1) – функция двух переменных.

(2) – уравнение связи.

1) Если можно разрешить (2) относительно 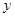: 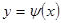, то, подставив в (1), получим функцию от одного переменного: нахождение условного экстремума сведётся к нахождению безусловного (обычного) экстремума функции от этой переменной.

2) Но можно поступить и иначе (что особенно ценно, когда (2) разрешить однозначно нельзя). При тех значениях 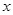, при которых функция имеет экстремум, производная от по 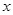должна обращаться в нуль. Считаем, что уравнение (2) определяет 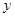как неявную функцию от 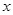. Считая, что 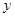есть функция от 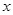, из (1) находим (как полную производную):

.

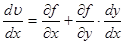Следовательно, в точках экстремума имеем

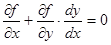. (3)

Из равенства (2) находим 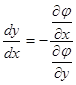(считаем 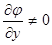), откуда

. (4)

Умножим члены равенства (4) на неопределённый пока коэффициент 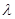(множитель Лагранжа)и сложим почленно (3) и полученное из (4):

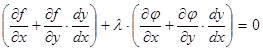
или 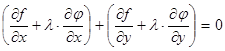(5)

((5) удовлетворяется во всех точках экстремума).

Подберём 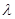так, чтобы для всех значени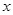й и 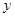, соответствующих экстремуму функции было 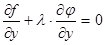, тогда и 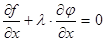при тех же значениях 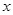и .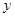

Таким образом, в точках экстремума должны одновременно удовлетворяться три уравнения с тремя неизвестными , , :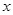

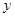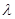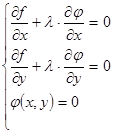(6)

Находим решение 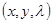, тогда точка ( 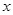, 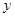) и будет точкой, подозрительной на условный экстремум ( 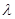больше не нужно!).

Обычно из характера самой задачи можно сказать есть ли в этой точке экстремум и какой?

Для удобства практического применения метода множителей Лагранжа и составления системы (6) сразу рассматривают функцию Лагранжа: .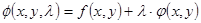

Тогда система 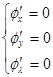и даёт систему (6).

II. Рассмотренный метод распространяется и на функции большего числа переменных, с большим числом уравнений связи.

Пусть нужно найти экстремум функции 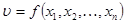при условии, что переменные удовлетворяют 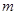уравнениям связи:

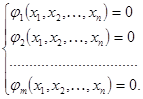
Тогда 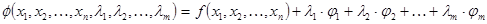– функция Лагранжа. Подозрительные на экстремум точки, находим, решая систему уравнений с неизвестными:

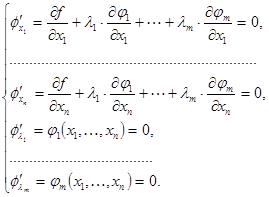
Пример. Найдём решение задачи о коробке, сформулированной вначале.

,

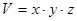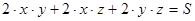
Составим функцию Лагранжа: .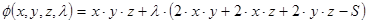

Напишем систему:

Домножим первое уравнение на 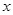, второе – на 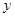, третье – на и почленно сложим их.

Получим:

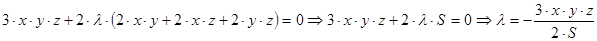Подставим это значение 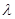в первые три уравнения, получим:

.

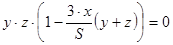
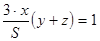
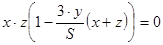
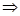
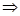
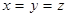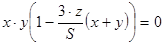
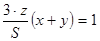
Из четвёртого уравнения тогда имеем: .

Отсюда: 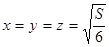, т.е. коробка должна быть кубом с ребром .

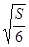§ 15. ОТЫСКАНИЕ ПАРАМЕТРОВ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ.

В результате проведения опытов, экспериментов получается таблица значений исследуемой величины 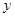(функции) в зависимости от наперёд заданных значений величины 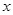(аргумента):

… …

… … .

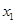
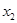
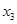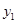
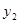
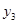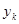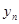Сразу пользоваться такой таблицей в дальнейших исследованиях нельзя, так как из многих опытов некоторые могли быть неудачными и соответствующие им табличные значения 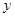ошибочны, далеки от верных. Чтобы иметь гарантию, что использование полученной таблицы не приведёт к большим ошибкам, таблицу математически обрабатывают. Основная идея обработки – подобрать формулу, хорошо описывающую табличные данные, а затем уже пользоваться ею так, как будто это настоящая функциональная зависимость 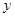от .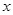

Как подбирают формулу по опытным данным?

Прежде всего по общему характеру опытных данных определяют общий вид формулы, а затем уже, используя отдельные опытные данные, определяют конкретные значения постоянных, входящих в формулу.

Чтобы представить вид формулы, очень полезно нанести табличные данные на график, после чего «от руки» на глаз провести через полученные точки наиболее правдоподобную кривую. При этом отдельные точки могут отстоять далеко от неё, большинство же – на ней или близко от неё. Тем самым сразу выявляются те данные таблицы, в которых можно подозревать большие ошибки.

При проведении кривой важно кроме экспериментальных точек использовать общие соображения о том, как должна вести себя кривая при значениях 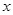, близких к , при больших значениях 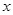, проходит ли кривая через начало координат, пересекает ли координатные оси, касается ли их и т.п.

Сравнивая построенную кривую с известными графиками функций, решают, к какой функции наиболее подходит функциональная зависимость 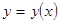. Выяснив общий вид формулы, выясняют значения констант, входящих в неё.

Рассмотрим это на примере.

Часто зависимость 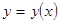бывает близка к линейной, т.е. график 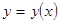близок к некоторой прямой. Для простоты будем считать, что при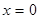 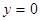, т.е. график и прямая проходят через начало координат. Тогда общий вид искомой формулы 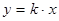.Коэффициент 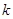нужно определить.

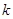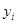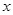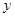Каждый опыт даёт своё значение : , и значения и в 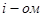опыте.

Казалось бы, что вполне может удовлетворить значение 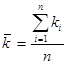, т.е. среднее арифметическое, и, соответственно, прямая .

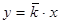Но в действительности это не так.

Так как опытные данные 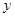отличаются от значения 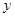по формуле на некоторую величину 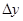, то ошибка в каждом опытном значении 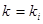будет 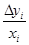. Чем меньше (ближе к нулю), тем больше ошибка в значении 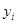скажется на 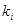. Отсюда следует, что меньшую ошибку в 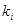дают опыты с большими значениями аргумента, на них и нужно ориентироваться. Во всяком случае среднее арифметическое не годится.

Встаёт вопрос: как определить то значение 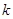, при котором функция 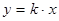наилучшим образом соответствует опытным данным?

Возьмём за меру отклонения функции 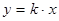от опытных данных в 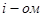эксперименте величину 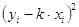/ можно было бы 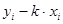, но она для разных может отличаться знаком и при нахождении суммы отклонений взаимно погашались бы, сумма отклонений была бы близка к нулю. Но сказать, что 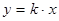хорошо описывает опытные данные всё равно было бы нельзя /. Величина 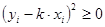всегда и такого погашения быть не может.

Мерой общей ошибки 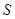в описании опытных данных функцией 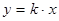считают сумму мер отклонений для всех опытов, т.е.

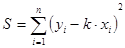(1)

Теперь задача сводится к отысканию такого 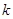, чтобы общее отклонение 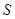было наименьшим. Если бы искомой формулой была не функция 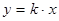, а другая – 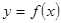, задача ставилась бы точно такая: найти константы, входящие в 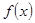так, чтобы общее отклонение 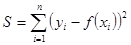было бы наименьшим.

Такой метод определения констант, входящих в формулу, называется методом наименьших квадратов.

Цель метода – уменьшить самые большие отклонения. Дело в том, что если даже одно 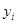отличается (уклоняется) от 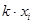, например, на 10 единиц, то в общем отклонении 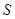это будет уже 100 единиц. А отклонение даже в 10 точках на 1 в общее отклонение внесут всего 10 единиц. Таким образом, на величину общего отклонения влияют сильно большие ошибки, малые, даже часто встречающиеся, влияют мало.

Как же конкретно находить константы по методу наименьших квадратов?

Рассмотрим случай формулы 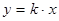. Исследуем на экстремум (минимум) функцию .

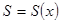Найдём 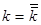, при котором

Отсюда 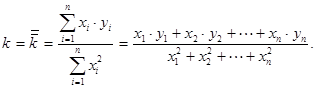(2)

Если случится, что все опытные точки лежат на одной прямой, т.е. 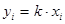, то из формулы (2) получаем

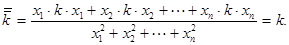
Если для различных опытов величина различна, то, подставляя в (2) 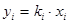, получим

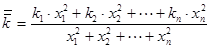(3)

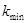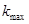Обозначим и – наименьшее и наибольшее среди .

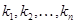Тогда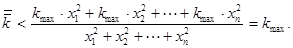

Аналогично .

Отсюда видно, что 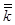является некоторым средним среди опытных 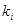, но находить его нужно по формуле (2) или (3), а не как среднее арифметическое.

Пусть теперь, например, известно, что график 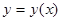не проходит через начало, но экспериментальные точки лежат на или близко от некоторой прямой. Тогда общий вид формулы будет .

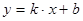Для определения 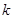и 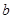снова можно применить метод наименьших квадратов. Величина 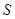в этом случае запишется формулой

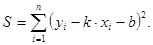
Выберем 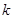и 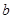так, чтобы 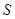было наименьшее. Для этого исследуем на экстремум функцию 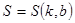– функцию двух переменных.

Найдём критическую точку

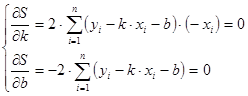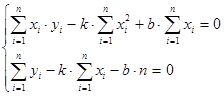или (4)

Обозначим для краткости

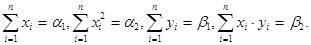
Тогда система (4) перепишется ,

Отсюда

Как уже сказано выше, и в случае более сложной зависимости 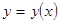, которую мы выбираем в виде формулы 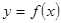, можно применять метод наименьших квадратов, хотя он и приводит часто к громоздким вычислениям.