Геометрический смысл модуля и аргумента производной
Производная  как функция комплексного переменного определяет отображение некоторой области
как функция комплексного переменного определяет отображение некоторой области 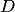 — области дифференцируемости функции
— области дифференцируемости функции 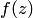 на область
на область  . В каждой точке
. В каждой точке 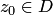 определено комплексное число
определено комплексное число  , следовательно, определены
, следовательно, определены 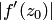 и
и 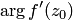 , если
, если 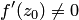 . Геометрически число
. Геометрически число 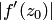 — длина радиус-вектора точки
— длина радиус-вектора точки  , a
, a 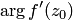 — угол наклона этого радиус-вектора к действительной оси. Возникает вопрос, как характеризуют эти величины само отображение
— угол наклона этого радиус-вектора к действительной оси. Возникает вопрос, как характеризуют эти величины само отображение 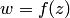 в точке
в точке  . Как известно, для функции действительной переменной аналогичный вопрос решается просто: производная
. Как известно, для функции действительной переменной аналогичный вопрос решается просто: производная  определяет угловой коэффициент касательной, проведенной к кривой
определяет угловой коэффициент касательной, проведенной к кривой 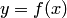 в точке
в точке 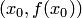 .
.
Рассмотрим геометрические свойства величин 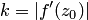 и
и  , полагая
, полагая 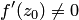 , а функцию
, а функцию 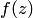 дифференцируемой в окрестности точки
дифференцируемой в окрестности точки  . Так как по определению производной
. Так как по определению производной  предел в точке не зависит от направления и способа стремления
предел в точке не зависит от направления и способа стремления  к нулю, то можно взять произвольную гладкую кривую
к нулю, то можно взять произвольную гладкую кривую 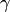 , проходящую через точку
, проходящую через точку  , и на ней любую точку
, и на ней любую точку  из окрестности точки
из окрестности точки  .
.
Образ кривой 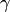 при отображении
при отображении 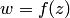 обозначим
обозначим 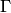 , образы точек
, образы точек  и
и  через
через 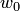 и
и 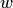 соответственно; из непрерывности отображения очевидно, что
соответственно; из непрерывности отображения очевидно, что 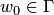 и
и 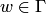 . Приращения переменных
. Приращения переменных 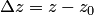 и
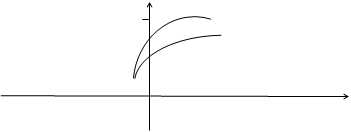
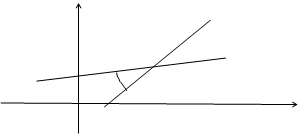
и 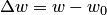 геометрически есть векторы (рис. 4.1), их длины —
геометрически есть векторы (рис. 4.1), их длины — 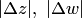 .
.

 | |||||
 | |||||
 | |||||
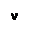
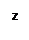
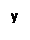

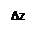


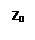

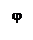




Из определения производной и свойства предела  имеем
имеем  , следовательно,
, следовательно, 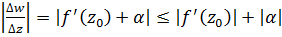 или
или  для
для 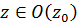 .Последнее неравенство, согласно определению, означает
.Последнее неравенство, согласно определению, означает  . Перепишем его следующим образом:
. Перепишем его следующим образом: 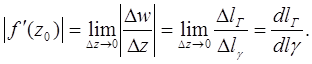
Где  и
и 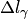 — длины соответствующих дуг кривых
— длины соответствующих дуг кривых 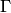 и
и 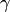 , как известно, эквивалентных стягивающим их хордам, если
, как известно, эквивалентных стягивающим их хордам, если 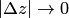
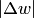 и
и 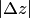 .
. 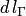 и
и  — элементы длин дуг
— элементы длин дуг 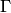 и
и 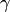 в точках
в точках 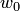 и
и  соответственно.
соответственно.
Отношение 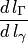 определяет изменение масштаба (растяжение, сжатие) в точке
определяет изменение масштаба (растяжение, сжатие) в точке  при отображении
при отображении 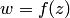 . В этом заключается геометрический смысл модуля производной. Величина
. В этом заключается геометрический смысл модуля производной. Величина 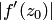 не зависит от вида кривой
не зависит от вида кривой 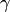 , поэтому отмеченное свойство имеет место и для любой другой гладкой кривой, проходящей через точку
, поэтому отмеченное свойство имеет место и для любой другой гладкой кривой, проходящей через точку  .
.
Следовательно, величина 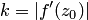 модуля производной есть величина постоянная для данной функции
модуля производной есть величина постоянная для данной функции 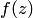 и данной точки
и данной точки  .
.
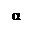

 Для аргумента производной имеет место равенство
Для аргумента производной имеет место равенство  , где
, где  и
и  — углы между действительными осями в плоскостях
— углы между действительными осями в плоскостях  и
и 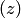 соответственно и касательными, проведенными к кривым
соответственно и касательными, проведенными к кривым 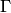 в точке
в точке 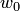 и
и 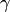 в точке
в точке  (рис.4.1).
(рис.4.1).
 |


Если точки 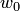 и
и  совместить, то
совместить, то 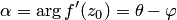 — угол поворота кривой
— угол поворота кривой 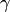 в точке
в точке  при отображении
при отображении 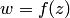 (рис.7.2). В этом заключается геометрический смысл аргумента производной аналитической функции.
(рис.7.2). В этом заключается геометрический смысл аргумента производной аналитической функции.





 Это свойство, очевидно, имеет место и для любой пары гладких кривых
Это свойство, очевидно, имеет место и для любой пары гладких кривых 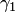 и
и 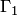 , проходящих через точки
, проходящих через точки  и
и 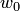 соответственно,
соответственно, 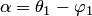 . Из равенств
. Из равенств 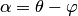 и
и 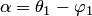 получаем
получаем 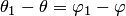 . Это означает, что угол
. Это означает, что угол  между кривыми
между кривыми 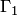 и
и 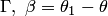 — равен углу между кривым
— равен углу между кривым 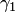 и
и 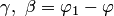 (рис. 4.3). Следовательно, при отображении сохраняются углы между кривыми.
(рис. 4.3). Следовательно, при отображении сохраняются углы между кривыми.
 |  | ||


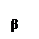


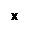
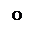


Отображение, сохраняющее углы между кривыми, называется конформным.
Дата добавления: 2015-10-09; просмотров: 1665;
