Геометрический смысл производной

Производная и дифференциал

Понятие производной

Пусть функция у = f(x) определена на промежутке X. Возьмем точку
х Î Х. Дадим значению х приращение Dх ¹ 0, тогда функция получит приращение D у = f(x + Dх) - f(x).

Производной функции у = f(x) называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю (если этот предел существует): .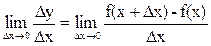

Производную также обозначают y' и dy/dx.

Геометрический смысл производной

Чтобы понять геометрический смысл производной, рассмотрим задачу о касательной.

Рассмотрим на плоскости график непрерывной функции у = f(x) (см. рисунок 3.1).

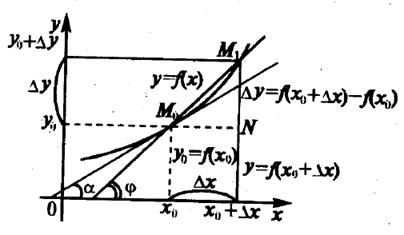
Построим касательную к этой кривой в точке М₀(х₀, у₀). Прежде всего, необходимо определить понятие касательной. Для этого дадим аргументу х₀ приращение Dх и перейдем на кривой у = f(x) от точки
М₀(х₀, f(x₀)) к точке М₁(х₀ + Dх, f(х₀ + Dх)). Проведем секущую М₀М₁. Под касательной к кривой у = f(x) понимают предельное положение секущей М₀М₁ при приближении точки М₁ к точке М₀, т.е. при Dх®0.

Угловой коэффициент секущей М₀М₁ (тангенс угла j наклона этой прямой к оси абсцисс) может быть найден из DМ₀М₁N: 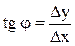. Тогда угловой коэффициент касательной (тангенс угла a) равен .

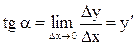Таким образом, производная функции представляет собой тангенс угла наклона касательной к графику функции к оси абсцисс (угловой коэффициент касательной).