Производная суммы, произведения и частного.

Нахождение производных по определению громоздко даже для простых функций, a тем более для сложных. Однако нахождение производных облегчают теоремы.

Теорема 1. Если функции u= ¦₁(х) и U= ¦₂(х) дифференцируемы в точке x, то и функция u ± U тоже дифференцируема в этой точке, причём y’=( u ± U)’= u’ ± U’. /производная алгебраической суммы равна алгебраической сумме производных /

Доказательство: Пусть у= u(х) ± U(х) и x - некоторая точка. Пусть _Dх – приращение аргумента в этой точке, х + _Dх – приращённое значение аргумента. Тогда каждая из функций u и U получит соответствующие приращения _D u _{и D} U и у+_D у= ( u +_D u) ±( U +_D U),

_Dу=[( u +_D u) ± ( U +_D U)]-[ u ± U]= _Du ± _DU ,

_Dу/ _Dх= _Du/ _Dх ± _DU/_Dх

lim_Dх_®0 (_Dу/ _Dх)= lim_Dх_®0 (_Du / _Dх) ± lim_Dх_®0 (_DU / _Dх) = u’ ± U’,

т.е y’= ( u ± U)’=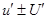

Пример: у= sin х + х² – 1, у^, = cos х + 2х.

Теорема 2.

Если функции u= ¦₁(х) и U= ¦₂(х) имеют производные в некоторой точке х, то и функция y=uU имеет производную в этой точке, причем у^,= (uU)^,= u^, U + uU^,:

Производная произведения равна производной 1-го сомножителя на 2-ой плюс производной 2-го на 1-ый.

Доказательство: аналогичное:

х- любая, _Dх- приращение, х + _Dх – приращённое значение аргумента, тогда

у + _Dу = (u+ _Du)( U + _DU)= uU+ u _DU+U_Du + _Du_DU;

_Dу= uU+ u _DU+U_Du + _Du_DU- uU= U_Du + u _DU + _Du_DU;

_Dу/ _Dх= U_Du/ _Dх + u _DU/_Dх + (_Du_DU)/_Dх;

lim_Dх_®0 (_Dу/ _Dх)= U lim_Dх_®0 (_Du / _Dх) + u lim_Dх_®0 (_DU / _Dх) + lim_Dх_®0 (_Du / _Dх) * lim_Dх_{®0 D}U, отсюда у^,= u^, U + uU^,, так как lim_Dх_{®0 D}U=0 в силу непрерывности функции U, как имеющей производную, а lim_Dх_®0 (_Du / _Dх)= u’¹¥.

Следствие: постоянный множитель можно выносить за знак производной, т.е. если у= с× u и производная u^, существует, то у^,= (с× u)^,= сu^,.

Доказательство: у^,= (с× u)^,= с^,× u + u^, × с= 0+ с× u^,= с× u^,

Примеры: 1. у^,=(3 sin х)^,= 3(sin х)^,= 3 cos х;

2. у^,= (х² cos х)= 2х cos х - х² sin х.

Замечание: Теоремы 1 и 2 можно применить для любого конечного числа дифференцируемых функций.

Например: (u × U× w)^,= u^,(U w)+ u(U w)^,= u^,U w + uU^, w+ uU w^, и т.п.

Теорема 3.

Если функции u= ¦₁(х) и U= ¦₂(х) имеют производные в точке х и функция U в точке х не равна нулю, то и функция у= u / U имеет производную в этой точке, причем у^,= (u / U)^,= (u^, U-uU^,)/ U²-производная дроби равна частному, числитель которой есть разность между производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель равен квадрату знаменателя данной дроби.

Доказательство обычное: х- любое, _Dх, х + _Dх, u+ _Du, U + _DU,

у + _Dу = (u+ _Du)/( U + _DU); _Dу= (u+ _Du)/( U + _DU)- u /U=

=((u+ _Du)U- u ( U + _DU)) /( U ( U + _DU))= (_DuU- u_DU)/ (U²+U_DU);

_Dу/ _Dх= (U_Du/ _Dх -u_DU/_Dх)/ (U²+U_DU);

lim_Dх_®0 (_Dу/ _Dх)= (U lim_Dх_®0 (_Du / _Dх)- u lim_Dх_®0 (_DU / _Dх))/ lim_Dх_®0(U²+U_DU) = (u^, U-uU^,)/ U², так как lim_Dх_®0(U_DU)= U lim_Dх_®0DU=0

(в силу непрерывности U, как имеющей производную)

Из теоремы (3) сразу найдем производные tqх и сtqх.

(tqх)^,= (sin х/ cos х)^,= ((sin х)^, cos х -sin х (cos х )^,)/cos² х=

(cos² х + sin² х)/ cos² х= 1/ cos² х;

tq’х= 1/ cos² х

(сtqх)^,= (cos х/ sin х)^,= ((cos х )^, sin х- (sin х)^, cos х)/ sin² х= -( cos² х + sin² х)/ sin² х= - 1/ sin² х;

(сtqх)^,= -1/ sin² х