Производные обратных тригонометрических функций.

у=arcsin х, у’^,=( arcsin х)’^,= 1/( 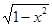), х ε (-1;1)

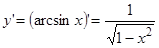
Функция у=arcsin х, х 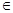(-1;1) есть обратная к функции х= sinу, определенной в (-p/₂, p/₂) по теореме (4), но 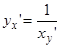и потому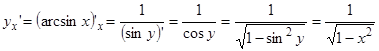

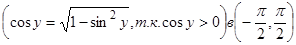
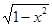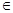у=arсcos х, у’= ( arccos х)’= -1/( ), х (-1;1)

Аналогично y’x = 1/x’y; y’x = ( arccos х)’=1/(cos y)’ =-1/sin y =

= -1/ 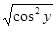= -1/( ),

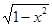3. у=arсtg х, у’= ( arctg х)’= 1/(1+х²), х (-¥ ; ¥)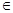

Функция y = arctg x обратна к x = tg y на (-п/2 , п/2),

при этом x’ = (tg y)’ = 1/ cos² у ¹0

Тогда y’x = 1/x’y, то y’=( arctg х)’ = 1/(tg y)’ = 1/(1/ cos² у) =

= 1/ (1+ tg ²y) = 1/ (1+х²)

4. у=arссtg х, у’= ( arcсtg х)’= -1/(1+х²),

(самостоятельно)

§9. Производные логарифмической и показательной функций.

y = ln x, y’ = (ln x)’ = 1/x .Возьмём произвольную точку x > 0 , дадим приращение Δx.

Вычислим Δy и составим отношение

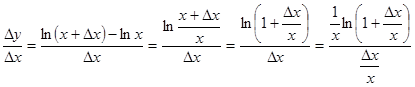
Перейдём к пределу: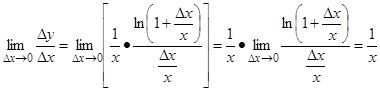

т.к 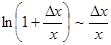. Итак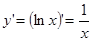

Пусть теперь 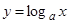, тогда: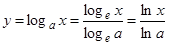

откуда 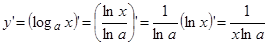, или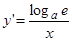

таким образом: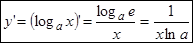

Для нахождения производной показательной функции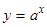

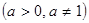
сначала прологарифмируем равенство, получим 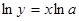. Теперь продифференцируем равенство по , считая, что 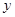-есть функция от и

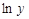-сложная функция от : ;

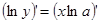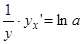
отсюда 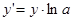или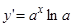

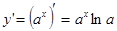
В частности при 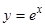, 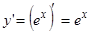т.к.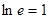

Замечание: Приём, применённый при нахождении производной показательной функции, называется логарифмическим дифференцированием функции, т.к. сначала находится производная логарифма, а затем уже производная самой функции.