Уравнение касательной и нормали к графику функции.

Пусть кривая есть график функции у= ¦(х). М (х₀, у₀) – произвольная точка на ней, в точке существует касательная.

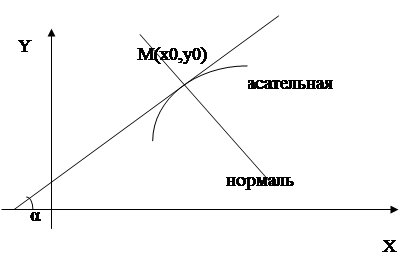Рис.5.

Определение: нормалью к кривой у= ¦(х) в точке М₀ называется прямая, проходящая через точку М₀ и перпендикулярна касательной в точке М₀ к этой кривой.

Напишем уравнение касательной и нормали, зная уравнение кривой и координаты точки М₀. Касательная имеет угловой коэффициент к= t_g 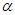= ¦^,(х₀). Из аналитической геометрии известно, что прямая имеет уравнение у- у₀= к( х – х₀).

Поэтому уравнение касательной: у - у₀= ¦^,(х₀)(х – х₀); (1)

Угловой коэффициент нормали К_н= 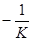(так как они перпендикулярны), но тогда уравнение нормали:

у- у₀=(-1/ ¦^,(х₀)( х – х₀); (2)

Если в точке не существует производная, то в этой точке не существует и касательная.

Например, функция ¦(х)=|х| в точке х=0 не имеет производной.

lim_Dх_®0 (_Dу/ _Dх)= lim_Dх_®0 (|_Dх|/ _Dх)=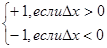

Односторонние пределы существуют, но lim_Dх_®0 (_Dу/ _Dх) не существует

y

y=|x|

Рис.6 x

Касательная тоже.

Такая точка называется угловой точкой графика.

§4. Связь между непрерывностью и дифференцируемостью функции.

Справедлива следующая теорема о дифференцируемой функции.

Теорема: если функция у= ¦(х) имеет конечную производную в точке х_0, то функция непрерывна в этой точке.

Доказательство:

Т.к. в точке х₀ существует производная ¦^,(х₀), т.е. существует предел

lim_Dх_®0 (_Dу/ _Dх)= ¦^,(х₀), то _Dу/ _Dх= ¦^,(х₀)+ 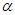, где

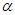- б.м.в., зависящая от _Dх. При _Dх®0, 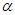®0, т.к. 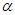= (_Dу/ _Dх) - ¦^,(х₀) ®0 при _Dх®0

Отсюда имеем: _Dу= ¦^,(х₀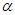) _Dх + _Dх.

Но тогда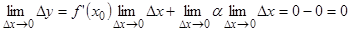

Бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, поэтому ¦(х) непрерывна в точке х₀.

Важно понять, что обратная теорема не верна!

Не всякая непрерывная функция является дифференцируемой.

Так, ¦(х) =|х| является непрерывной в точке х₀=0, график – сплошная линия, но ¦^,(0) не существует.

§5. Производные постоянной, синуса, косинуса и степенной функции.

1. у= ¦(х) =с; у^,= (с)^, = 0; (1)

Доказательство:

а) в любой точке х ¦(х) = с

б) дадим х приращение _Dх, х + _Dх, значение функции ¦ (х + _Dх)= с;

в) ¦ (х + _Dх)- ¦(х)= с- с= 0;

г) _Dу/ _Dх= 0/ _Dх = 0

д) lim_Dх_{®0 (D}у/ _Dх)= lim_Dх_®0 0 = 0

2. у= sin х; у^, = (sin х)^, = cos х; (2)

Доказательство:

а) в любой точке х ¦(х) = sin х;

б) дадим х приращение _Dх, х + _Dх, значение функции

¦ (х + _Dх)= sin (х + _Dх);

в) _Dу = sin (х + _Dх) - sin х = 2 sin (_Dх/ 2) * cos (х + (_Dх/ 2));

г) _Dу/ _Dх = ((sin (_Dх/ 2)) / (_Dх/ 2)) * cos (х + (_Dх/ 2));

lim_Dх_®0 ((sin (_Dх/ 2)) / (_Dх/ 2)) * cos (х + (_Dх/ 2))= 1 lim_Dх_®0(cos (х + (_Dх/ 2))= cos х (т.к. cos x – непрерывная функция).

1. Аналогично у= cos х, у^,= (cos х)^, = - sin х; (3)

2. у= хⁿ, n- целое положительное, у^,= (хⁿ)^,= n х^n-1,(4)

(Позднее формула будет доказана для любого n, не обязательно натурального).