Определение производной функции.

Задачи, приводящие к понятию производной функции.

а) Задача о скорости неравномерного прямолинейного движения (физическая)

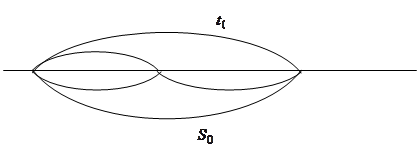Рис.1

Пусть материальная точка движется по прямой, начиная от т.0, неравномерно. За время t она пройдет некоторый путь S, т.е. S= ¦(t) - уравнение движения. Величина пройденного пути меняется в зависимости от времени. Какова скорость этого изменения?

Так как движение неравномерное, то обычное понимание скорости здесь неприемлемо. Здесь характеристикой движения является мгновенная скорость, скорость в данной точке.

Рассуждаем следующим образом: пусть в некоторый момент времени t₀, тело прошло уже путь S₀= ¦(t₀) и находилось в точке М₀, а в некоторый другой момент времени 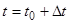оно прошло путь S = S₀+ _DS и находиться в точке М. За промежуток времени _Dt точка прошла путь _DS = S - S₀=¦(t) -¦(t₀)= ¦( t₀ + _Dt)- ¦(t₀) .

Если составить отношение _DS/_Dt, то оно даст среднюю скорость движения точки за время _Dt

V_ср= _DS/_Dt = (¦( t₀ + _Dt)- ¦(t₀))/ _Dt; (1)

Средняя скорость не может отразить всех колебаний в быстроте движения, она сглаживает их.

Чтобы узнать действительную скорость движения в некоторый момент t поточнее, нужно взять меньший промежуток времени _Dt.

Предел отношения _DS/_Dt при _Dt®0 и называется скоростью движения в данный момент времени t_0.

V=lim_Dt®0(_DS/_Dt)= lim_Dt®0 ((¦( t₀ + _Dt)- ¦(t₀))/ _Dt); (2)

Таким образом, для нахождения скорости точки в данный момент времени нужно уметь находить предел вида (2).

б) Задача о касательной к кривой (геометрическая).

М

Т

L

М₀ Рис.2

Дадим, прежде всего, само определение касательной к кривой в некоторой точке. Пусть дана кривая L и точка М₀ на ней. Возьмем на L другую точку М и проведем секущую М₀М. При изменении положения точки М на кривой L, положение секущей будет тоже меняться. Если при неограниченном приближении точки М по кривой к точке М₀ с любой стороны секущая М₀М стремиться занять положение некоторой определенной прямой М₀Т, то эта прямая М₀Т и называется касательной к кривой L в точке М₀.

		М0(x0,y0)
	y0   y

M(x,y)   Dx

Рис.3

Введя это определение, рассмотрим задачу о проведении касательной к данной кривой L, являющейся графиком непрерывной функции в обычной прямоугольной системе координат: .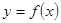

Допустим, что кривая L в точке М (x₀, y₀) имеет касательную М₀Т, которая составляет с положительным направлением оси ОХ угол 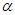¹±p/2.

Задача проведения касательной окажется решенной, если суметь найти угол 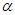или все равно угловой коэффициент касательной М₀Т: К₀= =t_g .

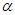Для решения задачи поступаем следующим образом:

на L возьмем произвольную точку М, близкую к точке М₀.

Координаты т.М (х,у)= М (х₀ + _Dх, у₀ + _Dу), здесь _Dх – приращение аргумента x в x₀, _Dу – соответствует приращение функции.

Проведем секущую М₀М, она образует с положительным направлением оси ОХ угол φ, ее угловой коэффициент к= t_gφ. Из прямоугольного треугольника ММ₀Р имеем

к= t_gφ =_Dу/_Dх, но так как у=¦(х),

_Dу=¦(х)- ¦(х₀) = ¦(х₀ + _Dх)- ¦(х₀).

Поэтому, к= (¦(х₀ + _Dх)- ¦(х₀))/ _Dх. Если устремить _Dх к нулю, то по определению непрерывной функции 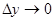тоже, а значит, точка М приближается к точке М₀. Но тогда секущая приближается к положению касательной и угловой коэффициент секущей стремится к угловому коэффициенту касательной К₀.

Таким образом, 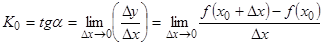; (3)

Снова пришли к необходимости вычислять пределы вида (3). Так как многие задачи приводят к пределам вида (2) и (3), то их и стали рассматривать в общем, виде.

Определение производной функции.

Пусть функция у=¦(х) определена в некотором промежутке Х (например, интервале или сегменте).

Проведем следующие действия:

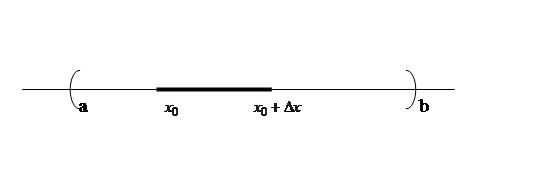1. Возьмем произвольную точку х₀ÎХ и вычислим значение функции в ней у₀=¦(х₀)

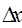
Рис.4

2. Дадим аргументу х в точке х₀ произвольное приращение _Dх¹0 (_Dх_<^>0), но так, чтобы х = х₀ + _DхÎХ. Вычислим значение функции в приращенной точке х= х₀ + _Dх, у = у₀ + _Dу= ¦ (х₀ + _Dх).

3. Найдем приращение функции, соответствующее данному приращению _Dх аргумента

_Dу= у – у₀ = ¦ (х₀ + _Dх)- ¦(х₀)

4. Составим отношение _Dу/_Dх = (¦ (х₀ + _Dх)- ¦(х₀))/ _Dх; (1)

5. В полученном отношении (1) перейдем к пределу при _Dх®0

lim_Dх_®0 (_Dу/ _Dх)= lim_Dх_®0 (( ¦ (х₀ + _Dх)- ¦(х₀))/ _Dх); (2)

если он существует, то он и называется производной функции в точке х₀, обозначается ¦^,(х₀)

Определение: Производной функции в некоторой точке х₀ называется предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента _Dх®0, т.е.

¦^,(х₀) = lim_Dх_®0 (_Dу/ _Dх), или

¦^,(х₀) = lim_Dх_®0 ((¦ (х₀ + _Dх)- ¦(х₀))/ _Dх);

Применяются и другие обозначения.

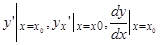и др.

Если производная находится в произвольной точке хÎХ, то она есть уже функция от х на Х и обозначается просто ¦^,(х), у^,, у^,_{х ……}

Если предел (2) не существует, говорят, что функция не имеет производной в точке х₀.

Если предел (2) = ¥, то иногда говорят, что в точке х₀ функция имеет бесконечную производную.

Функция, имеющая в точке конечную производную, называется дифференцируемой в этой точке, а операция нахождения производной называется операцией дифференцирования функции.

Пример: Найти производную функции ¦(х) = 3х² + 1

а) в произвольной точке х₀Î(-¥, ¥);

б) в точке х₀ = 2;

1) х₀, ¦(х₀) = 3х²₀ + 1;

2) х₀ + _Dх, ¦ (х₀ + _Dх)= 3 (х₀ + _Dх)²+ 1 = 3х²₀+ 6х_0Dх + 3_Dх² + 1

3) _Dу= ¦ (х₀ + _Dх)- ¦(х₀)= 3х²₀+ 6х_0Dх + 3_Dх² + 1 - 3х²₀ – 1= 6х_0Dх + 3_Dх^2;

_Dу/ _Dх= 6х₀ + 3_Dх;

4) lim_Dх_®0 (_Dу/ _Dх)= lim_Dх_®0 (6х₀ + 3_Dх) = 6х₀.

Итак, ¦^,(х₀)= 6х₀; в точке х₀= 2 вычисляем сразу же:

¦^,(2)= 6*2= 12

Если вернуться к рассмотренным двум задачам, то можно заметить следующее:

Мы видели, что уравнение пути при неравномерном прямолинейном движении S= ¦(t) и его скорость в данный момент времени t₀ есть

V=lim_Dt®0(_DS/_Dt)= lim_Dt®0 ((¦( t₀ + _Dt)- ¦(t₀))/ _Dt

Из сказанного ясно, что 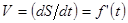, т.е. скорость прямолинейного неравномерного движения есть производная пути по времени (механический смысл производной).

Геометрический смысл производной вытекает из задачи о касательной. Угловой коэффициент касательной к кривой у=¦(t), к= t_g 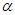= lim_Dх_®0 (_Dу/ _Dх), т.е. к= t_g 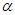= ¦’ (х₀); откуда видим, что геометрически производная функции представляет угловой коэффициент касательной к графику функции у= ¦(x) в точке, абсцисса которой является точкой дифференцирования функции.

Заметим, что с помощью производной можно определить понятия удельной теплоемкости вещества, плотности вещества, силы тока и др.