Производные обратной и сложной функций.
Теорема 4. (О производной обратной функции).
Если для функции у= ¦(х) существует обратная функция х= j(у), которая в некоторой точке у имеет производную j,(у) ¹0, то в соответствующей точке х функция у= ¦(х) имеет производную ¦,(х) равную 1/ j,(у), т.е. ¦,(х)= 1/ j,(у).
Доказательство: рассмотрим функцию х= j(у), дадим аргументу у приращение Dу¹0, тогда функция х получит приращение Dх= j(у+ Dу)- j(у); Dх¹0, так как если бы Dх=0, то х + Dх=х и Dу= ¦(х+Dх )- ¦(х)=0, чего нет.
Тогда Dу/ Dх= 1/ (Dх/ Dу); (1)
Так как функция j(у) имеет производную, то она непрерывна в точке у, но тогда при Dу®0 и Dх®0.
Перейдем к пределу при Dу®0:
limDх®0 (Dу/ Dх)= limDу®0 (1/ (Dх/ Dу))= 1/limDy®0 (Dх/ Dу)= 1/ x’ y,
т.е. y’ x=1/x’ y , или f’(x)=1/j’(у)
Теорема 5. (производная сложной функции).
Если функция u = j(х) имеет в некоторой точке х производную u,х = j,(х), а функция у= ¦( u) в соответствующей точке u = j(х) производную у,= ¦,(u), то и сложная функция у= ¦[j(х) ] в точке х имеет производную, равную произведению производных функции ¦( u) и j(х):
[¦(j(х))], = ¦,u(j(х))· j,х(х) или короче у,х= у,u· u,х.
Коротко: производная сложной функции равна произведению её производной по промежуточному аргументу на производную промежуточного по основному.
Доказательство: дадим х приращение Dх. Тогда функция u получит соответствующее приращение Du. В свою очередь функция у получит приращение Dу. Причем, при Dх®0 и Du ®0 и Dу®0. Так как
lim Du ®0 (Dу/Du )= ¦ ’(u), то Dу= ¦,(u) Du+ 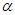 Du, где
Du, где 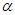 ®0 при Du ®0.
®0 при Du ®0.
Разделим равенство почленно на Dх и перейдем к пределу к пределу при Dх®0
limDх®0 (Dу/ Dх)= ¦,(u) limDх®0 (Du / Dх)+ limDх®0 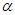 · limDх®0 (Du / Dх)=
· limDх®0 (Du / Dх)=
¦,(u) · j,(х)+ 0· j,(х)= ¦,х(u) · j,х(х), откуда ¦,х[j(х)]= ¦,u[j(х)] · j,х(х).
Замечание. Если промежуточных аргументов несколько, то формула аналогична.
Например, у= ¦( u), u= j(t), t= y(х); тогда
у' х= у’u· u’t · t’х
Пример: y=tg sin 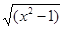 , y=tg υ, υ=sin z, z=
, y=tg υ, υ=sin z, z= 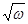 , ω= х2 –1
, ω= х2 –1
y’x =y’ v υ’z z’ω ω’x = (1/cos2 υ) cos z ½ ω -½ 2x =
= (cos 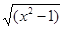 x) / (cos2 sin
x) / (cos2 sin 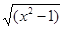
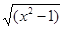 )
)
Обычно в виде цепочки представляют мысленно и сразу заменяют промежуточные аргументы их выражениями через основной.
у' х = (1/cos2 sin 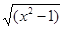 ) (x cos
) (x cos 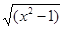 /
/ 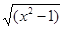 ) –получим прежнее выражение.
) –получим прежнее выражение.
Дата добавления: 2015-10-05; просмотров: 774;
