Функции и степенно-показательной функции.

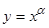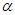, где - любое постоянное действительное число .

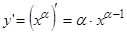Применим операцию логарифмического дифференцирования: ,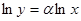

, , ,

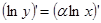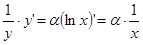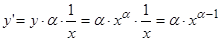т.е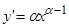

Например: , .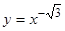

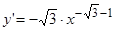Пусть имеем функцию 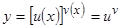, показатель и основание которой есть функции от . Такую функцию называют степенно-показательной (или иногда сложной показательной).

Докажем, что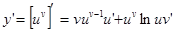

Применим операцию логарифмического дифференцирования 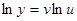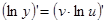, , 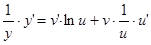отсюда ,

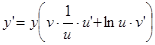или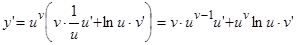

Правило: производная степенно-показательной функции равна сумме двух слагаемых, первое из них получается, если дифференцируем функцию как степенную, считая 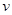постоянным, второе –если дифференцировать функцию как показательную, считая 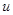постоянным.