Дифференциал функции. Пусть функция определена в некотором промежутке и в некоторой внутренней точке имеет конечную производную
Пусть функция 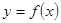 определена в некотором промежутке
определена в некотором промежутке 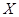 и в некоторой внутренней точке
и в некоторой внутренней точке 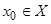 имеет конечную производную
имеет конечную производную 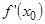 . Тогда
. Тогда 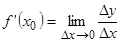 , где
, где 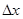 -приращение аргумента
-приращение аргумента  в данной точке
в данной точке 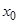 , а
, а 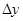 -соответствующее ему приращение функции. Можем записать:
-соответствующее ему приращение функции. Можем записать:  (1).
(1).
где 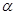 -б.м.в, зависящая от
-б.м.в, зависящая от 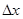 ,
, 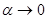 при
при 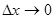 . Оба слагаемых в правой части (1) являются величинами б.м., они
. Оба слагаемых в правой части (1) являются величинами б.м., они 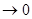 при
при 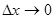 . Первое слагаемое
. Первое слагаемое 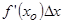 является б.м. одного порядка малости с
является б.м. одного порядка малости с 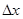 , т.к.
, т.к. 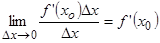 - определённое число (полагаем
- определённое число (полагаем 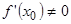 ). Второе слагаемое – есть величина б.м. высшего порядка малости по сравнению с
). Второе слагаемое – есть величина б.м. высшего порядка малости по сравнению с 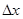 , т.к.
, т.к. 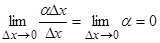 ,
, 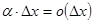 . Таким образом, приращение функции можно записать
. Таким образом, приращение функции можно записать 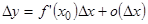 . Последняя запись отчётливо показывает, что величина приращения функции
. Последняя запись отчётливо показывает, что величина приращения функции 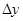 в основном зависит от первого слагаемого, оно, как бы, содержит в себе главную часть приращения функции, второе же содержит незначительную часть приращения функции. Поэтому
в основном зависит от первого слагаемого, оно, как бы, содержит в себе главную часть приращения функции, второе же содержит незначительную часть приращения функции. Поэтому 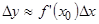 . Ввиду особой роли произведения
. Ввиду особой роли произведения 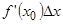 , для него введено специальное название – дифференциала функции и символическое обозначение
, для него введено специальное название – дифференциала функции и символическое обозначение  .
.
Определение: Дифференциалом функции 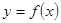 в некоторой точке
в некоторой точке 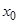 называют произведение производной функции в этой точке на приращение аргумента. Если вычисляют
называют произведение производной функции в этой точке на приращение аргумента. Если вычисляют 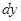 в произвольной точке
в произвольной точке  , то обозначают
, то обозначают 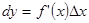 . Тогда
. Тогда 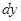 -есть переменная величина от
-есть переменная величина от  .
.
Замечание: Выделение дифференциала как главной части приращения функции вызвано ещё и тем, что дифференциал к тому же есть и линейная часть приращения функции отоносительно 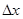 (т.е. содержит
(т.е. содержит 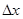 в первой степени), что очень удобно в приближённых вычислениях. При малых
в первой степени), что очень удобно в приближённых вычислениях. При малых 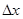
 или
или 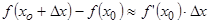 или
или 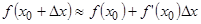 (2).
(2).
Например: вычислить 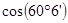 Пользуемся формулой (2), считая
Пользуемся формулой (2), считая 
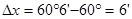 . Тогда
. Тогда 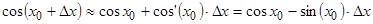 . Градусную меру переведём в радианную
. Градусную меру переведём в радианную 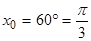 ,
, 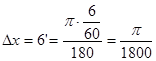 . Имеем
. Имеем 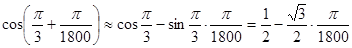
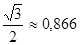 ,
, 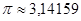
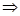

Мы говорим о дифференциале функции 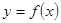 . Выясним вопрос о дифференциале независимой переменной
. Выясним вопрос о дифференциале независимой переменной  . Рассмотрим функцию
. Рассмотрим функцию 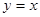 . В этом случае дифференциал функции будет одновременно и дифференциалом независимой переменной
. В этом случае дифференциал функции будет одновременно и дифференциалом независимой переменной 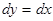 . Но
. Но 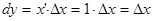
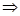
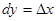 и пэтому
и пэтому 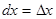 . Таким образом:
. Таким образом:
Дифференциалом независимой переменной можно считать её приращение: 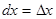 .
.
Поэтому для дифференциала функции применяется обычно запись: 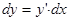 или
или 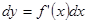 (3)
(3)
Из (3) следует, что 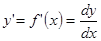 , т.е. производную функции можно рассматривать как частное от деления дифференциала функции на дифференциал аргумента, а не просто как единый символ производной
, т.е. производную функции можно рассматривать как частное от деления дифференциала функции на дифференциал аргумента, а не просто как единый символ производной 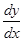 , как считалось до сих пор.
, как считалось до сих пор.
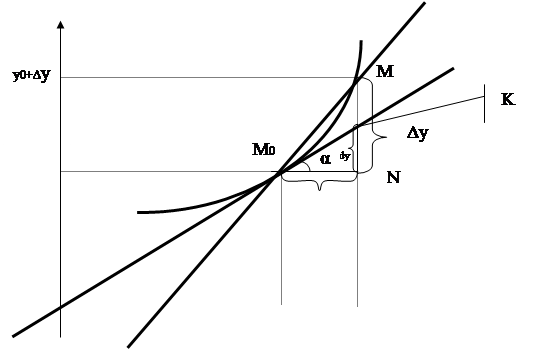
Выясним геометрический смысл дифференциала функции.
Пусть задана функция 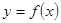 . Начертим её график.
. Начертим её график.
 |
y0
|
|
|
 | |||||||||
|
|
| |||||||
На нём возьмём точку 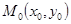 . Через точку
. Через точку 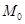 проведём касательную
проведём касательную 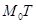 . Как мы видим, её угловой коэффициент
. Как мы видим, её угловой коэффициент 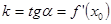 . Если абсциссе
. Если абсциссе  в точке
в точке 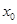 дать приращение
дать приращение 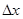 , то функция
, то функция 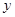 в точке
в точке 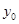 получит приращение
получит приращение 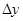 . Отметим на графике точку
. Отметим на графике точку 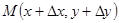 . Проведём секущую
. Проведём секущую 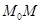 и рассмотрим
и рассмотрим 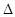
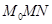 .Видим, что
.Видим, что  ,
, 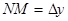 ,
, 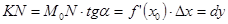 .
.
Вывод: в то время как 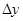 -есть приращение ординаты точки на кривой,
-есть приращение ординаты точки на кривой, 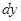 -есть приращение ординаты точки на касательной к этой кривой в точке
-есть приращение ординаты точки на касательной к этой кривой в точке 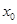 . Из чертежа наглядно видно – чем меньше
. Из чертежа наглядно видно – чем меньше 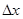 , тем меньше отрезок
, тем меньше отрезок 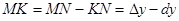 , т.е. при малых
, т.е. при малых 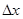
 , что уже отмечалось выше.
, что уже отмечалось выше.
Дата добавления: 2015-10-05; просмотров: 564;
