Дифференциал основных элементарных функций, суммы, произведения и частного.
Способ нахождения дифференциала сразу следует из определения: Чтобы найти дифференциал функции, достаточно вычислить производную этой функции и умножить её на дифференциал независимого переменного.
В связи с этим все формулы для производных легко преобразуются в формулы для дифференциала.
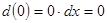 ;
;
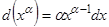 ;
;
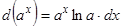 ;
;
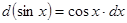 ;
;
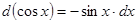 ;
;
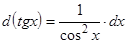 ;
;
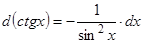 ;
;
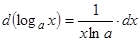 ;
;
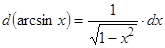 ;
;
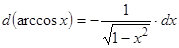 ;
;
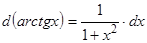 ;
;
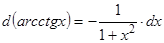 ;
;
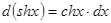 ;
;
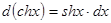 ;
;
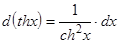 ;
;
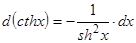 ;
;
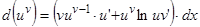
Легко для случая дифференциала доказываются и некоторые общие правила:
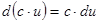 ;
;
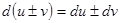 ;
;
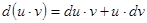 ;
;
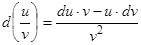 .
.
Доказательство всех аналогично.
Например(4):
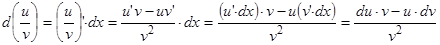
(Остальные самостоятельно.)
§17. Дифференциал сложной функции. Инвариантность (неизменность) формы дифференциала функции.
Мы видели, что дифференциал функции 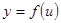 может быть записан в виде:
может быть записан в виде: 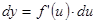 (1),
(1),
если 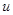 есть независимая переменная. Пусть теперь
есть независимая переменная. Пусть теперь 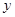 есть сложная функция от
есть сложная функция от  , т.е.
, т.е. 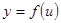 ,
, 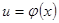 и поэтому
и поэтому 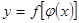 . Если производные функций
. Если производные функций 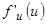 и
и 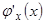 существуют, то
существуют, то 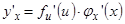 , как производная сложной функции. Дифференциал
, как производная сложной функции. Дифференциал 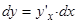 или
или 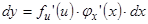 . Но
. Но 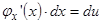 и поэтому можем записать
и поэтому можем записать 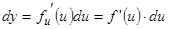 , т.е. получили снова выражение для
, т.е. получили снова выражение для 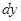 как и в (1).
как и в (1).
Вывод: формула (1) верна как и в случае, когда 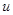 есть независимая переменная, так и в случае, когда
есть независимая переменная, так и в случае, когда 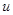 есть функция от независимой переменной
есть функция от независимой переменной  . В первом случае под
. В первом случае под 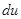 понимается дифференциал независимой переменной
понимается дифференциал независимой переменной 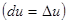 , во втором – дифференциал функции (при этом
, во втором – дифференциал функции (при этом 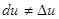 , вообще говоря). Это свойство сохранения формы (1) и называется инвариантностью формы дифференциала.
, вообще говоря). Это свойство сохранения формы (1) и называется инвариантностью формы дифференциала.
Инвариантность формы дифференциала даёт большие выгоды при вычислении дифференциалов сложных функций.
Например: нужно вычислить 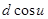 . Независимо от того, зависимая или независимая переменная
. Независимо от того, зависимая или независимая переменная 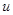 , мы можем записать
, мы можем записать 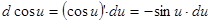 . Если
. Если 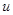 - функция, например
- функция, например 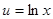 , то найдём
, то найдём 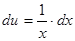 и, пользуясь инвариантностью формы дифференциала, имеем право записать
и, пользуясь инвариантностью формы дифференциала, имеем право записать 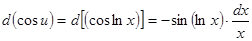 .
.
Дата добавления: 2015-10-05; просмотров: 1174;
