Правило Лопиталя.
При нахождении пределов функции мы широко пользовались теоремами о пределах суммы, разности, произведения, частного и возможностью предельного перехода под знаком непрерывной функции.
Однако, когда под знаком предела оказывалось выражение, представляющее неопределенность вида 0/0, 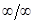 ,
, 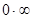 ,
, 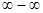 и т.п. теоремы о пределах уже были неприменимы и приходилось в каждом отдельном случае по-своему раскрывать эти неопределенности. Понятие производной дает очень удобное правило раскрытия неопределенностей, называемое правилом Лопиталя. Сформулируем его в виде теоремы.
и т.п. теоремы о пределах уже были неприменимы и приходилось в каждом отдельном случае по-своему раскрывать эти неопределенности. Понятие производной дает очень удобное правило раскрытия неопределенностей, называемое правилом Лопиталя. Сформулируем его в виде теоремы.
Теорема Лопиталя.
Пусть функции ¦(х) и 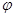 (х) при
(х) при 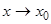 ( или
( или 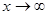 ) одновременно стремятся к нулю или бесконечности. Если отношение их производных имеет предел, то отношение самих функций также имеет предел, равный пределу отношения производных, т.е.
) одновременно стремятся к нулю или бесконечности. Если отношение их производных имеет предел, то отношение самих функций также имеет предел, равный пределу отношения производных, т.е.
limх®х0 ¦(х) = limх®х0 ¦1(х) (1)
φ(x) φ1(х)
Общее доказательство теоремы очень громоздко (опирается на теорему Коши).
Приведём лишь доказательство одного простого случая и рассмотрим часто встречающиеся случаи применения теоремы.
Докажем, что если 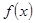 и
и 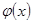 определены и непрерывны в окрестности
определены и непрерывны в окрестности 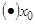 ,при
,при 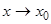 они стремятся к нулю и их производные в точке
они стремятся к нулю и их производные в точке 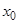 существуют, причём
существуют, причём 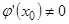 , то
, то 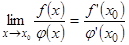 (2).
(2).
Доказательство: Т.к. 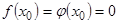 (следует из условия теоремы), то
(следует из условия теоремы), то 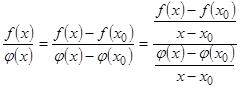 . Переходя к пределу при
. Переходя к пределу при  и используя теорему о пределе дроби, получим:
и используя теорему о пределе дроби, получим: 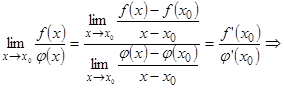 следует (2).
следует (2).
Примеры: 1). limх®0 sin 5х = lim х®0 (sin 5х)1 = 5cos0 = 5
2х (2х)1 2 2
2). Lim х®0 ех – cos х = limx 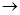 0 ех + sinх = 1 = 1
0 ех + sinх = 1 = 1
х 1 1
Возможно, что предел отношения производных равен  ,
,
тогда и предел отношения функции тоже равен  .
. 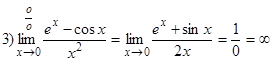
Может оказаться, что предел отношения производных снова есть неопределенность 0/0. Тогда применяем правило Лопиталя еще раз.
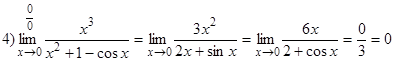
Замечание 1. Формула (1) написана при 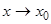 , но она верна и при
, но она верна и при 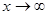 ,
, 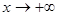 ,
, 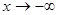 .
.
Положим 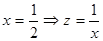 , тогда при
, тогда при 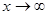 ,
, 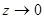 , можем применить формулу (1):
, можем применить формулу (1): 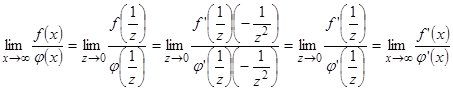 , т.е
, т.е 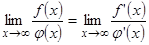 (1*).
(1*).
Аналогично при 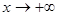 ,
, 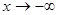 .
.
Пример 6:
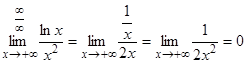
Замечание 2: Как видим при раскрытии неопределенностей правило Лопиталя приходится иногда применять несколько раз подряд, если после каждого снова получается неопределенность.
Если неопределенности нет, то правило применять нельзя, возможна ошибка.
Пример: lim х®0 2х3 + 3х + 1 , сразу видно, что lim равен -1
х2 + 4х – 1
по правилу Лопиталя нашли бы 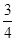 - Ошибка!
- Ошибка!
Замечание 3. Теорема Лопиталя дает лишь достаточное условие существование предела отношения функций. Если предел отношения производных не существует, то это еще не значит, что и предел отношения функций тоже не существует, просто, нужно раскрывать не по правилу Лопиталя, а другим способом.
Пример: lim х®  х+ sin х = lim х®
х+ sin х = lim х®  1 + cos х = lim х®
1 + cos х = lim х®  ( 1+ cos х) – не
( 1+ cos х) – не
х 1
существует.
Однако, легко иначе
lim х®  х+ sin х = lim х®
х+ sin х = lim х®  ( 1 + sin х) = 1 + 0 = 1
( 1 + sin х) = 1 + 0 = 1
х х
Правило Лопиталя применимо к раскрытию неопределенностей вида 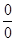 и
и 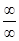 . Легко показать, что все остальные к ним сводятся.
. Легко показать, что все остальные к ним сводятся.
Покажем это.
0 · 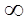 : Имеем ¦(х) ·
: Имеем ¦(х) · 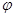 (х), причем при
(х), причем при 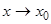 ,
, 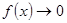 ,
, 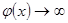 . Тогда поступают так
. Тогда поступают так
 , т.е. приходим от
, т.е. приходим от 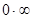 к
к 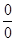 или
или 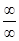 и применяется правило Лопиталя.
и применяется правило Лопиталя.
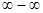 : Имеем
: Имеем 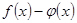 , причем, при
, причем, при 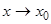 ,
, 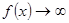 ,
, 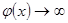 . Тогда поступим так:
. Тогда поступим так:
 получаем неопределенность
получаем неопределенность 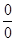 и можем применить правило Лопиталя.
и можем применить правило Лопиталя.
Пример: 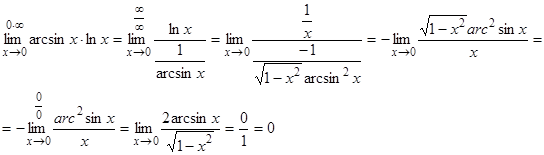
Кроме четырех неопределенностей 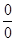 ,
, 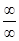 ,
, 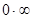 ,
, 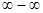 , имеются и три неопределенных выражения, получающихся из степенно-показательной функции:
, имеются и три неопределенных выражения, получающихся из степенно-показательной функции:
Это 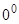 ,
, 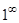 и
и 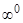
00 – это неопределенное выражение вида [¦(х)] φ(x) при х 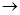 х0
х0
если  , и
, и 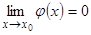 . Соответственно понимаются и остальные два. Эти три неопределенности легко сводятся логарифмированием к неопределенности вида 0·
. Соответственно понимаются и остальные два. Эти три неопределенности легко сводятся логарифмированием к неопределенности вида 0·  , которая уже раскрывается по правилу Лопиталя.
, которая уже раскрывается по правилу Лопиталя.
Пример: 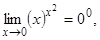
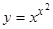 ,
, 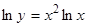 ,
, 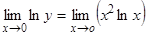 .
.
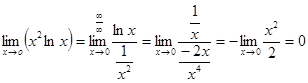
Итак, 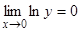 или
или  , т.е.
, т.е. 
В заключение покажем, что показательная функция ах растет быстрее, а логарифм loqaх медленнее, чем степенная 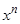 , при
, при  .
.
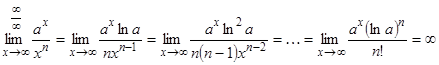
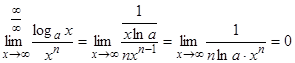
Дата добавления: 2015-10-05; просмотров: 1160;
