Производные высших порядков.

Пусть функция у= ¦(х) дифференцируема на некотором проме­жутке Х, (т.е. имеет конечную производную у¹=¦¹(х) в каждой точке этого промежутка). Тогда ¦¹(х) есть в Х сама функция от х. Может оказаться, что в некоторых точках или во всех х ¦¹(х) сама имеет производную, т.е. существует производная от производной (у¹)¹=(¦¹(х)¹. В этом случае ее называют второй производной или производной второго порядка. Обозначают символами у¹¹,¦¹¹(х), d²у/ dх². Если нужно подчеркнуть, что производная находится в т.х₀, то пишут

у¹¹/х=х₀ или ¦¹¹(х₀) или d²у/ dх²/х=х₀

производная у¹ называется производной первого порядка или первой производной.

Итак, производной второго порядка называют производную от производной первого порядка функции.

Совершенно аналогично, производная (там, где она существует) от производной второго порядка называется производной третьего порядка или третьей производной.

Обозначают (у¹¹)¹= у ¹¹¹=¦¹¹¹(х)= d³у/ dх³= d³¦(х) / dх³

Вообще производной n-го порядка функции у= ¦(х) называется производная от производной (n-1) порядка этой функции. (если они существуют, конечно).

Обозначают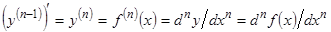

Читают: n-ая производная от у, от ¦(х); d n у по d х в n-ой.

Четвертый, пятый и т.д. порядок неудобно обозначать штрихами, поэтому пишут число в скобках, вместо ¦^v(х) пишут ¦⁽⁵⁾(х).

В скобках, чтобы не путать n-ый порядок производной и n-ую степень функции.

Производные порядка, выше первого, называют производными высших порядков.

Из самого определения следует, что для нахождения n-ой производной нужно найти последовательно все предыдущие от 1-ой до (n-1)-ой.

Примеры: 1) у=х⁵; у¹=5х⁴; у¹¹=20х³;

у¹¹¹=60х²; у⁽⁴⁾=120х; у⁽⁵⁾=120; у⁽⁶⁾=0,…

2) у=е^х; у¹=е^х; у¹¹=е^х;…;

3) у=sinх; у¹=cosх; у¹¹= -sinх; у¹¹¹= -cosх; у⁽⁴⁾= sinх;…

Заметим, что вторая производная имеет определенный механический смысл.

Если первая производная пути по времени есть скорость прямолинейного неравномерного движения

V=ds/dt, где S=f(t) – уравнение движения, то V¹=dV/dt= d² S/dt²-есть скорость изменения скорости, т.е. ускорение движения:

a= f¹¹(t)= dV/dt= d² S/dt².

Итак, вторая производная пути по времени ,есть ускорение движения точки – в этом состоит механический смысл второй производной.

В ряде случаев удается написать выражение производной любого порядка, минуя промежуточные.

Примеры:

у=е^х; (у)⁽ⁿ⁾=(е^х)⁽ⁿ⁾=е^х;

у=а^х; у¹=а^хlnа; у¹¹=а^х(lnа)²; у⁽ⁿ⁾=а^х(lnа)ⁿ;

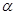у=х^α; у¹= αx^α-1; у¹¹= ; у^(п)= α(α-1)… (α-n+1)x ^α-n, при =n имеем

у^(п)=(х^п)^(п)= n! Производные порядка выше n все равны нулю.

у= sinх; у¹=cosх; у¹¹= -sinх; у¹¹¹= -cosх; у⁽⁴⁾= sinх;… и т.д.. Т.к.

у¹= sin(х+ 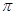/2); у¹¹= sin(х+2 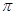/2); у¹¹¹= sin(х+3 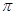/2); и т.д., то у^(п)=( sinх)^(п)= sin(х+n 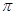/2).

Легко установить последовательным дифференцированием и общие формулы:

1) (СU)⁽ⁿ⁾= С(U) ⁽ⁿ⁾; 2) (U±V) ⁽ⁿ⁾ = U⁽ⁿ⁾ ± V⁽ⁿ⁾

Более сложной оказывается формула для n-ой производной от произведения двух функций (U·V) ⁽ⁿ⁾. Она носит название формулы Лейбница.

Получим ее

у= U·V; у¹= U ¹V+ UV¹; у¹¹= U ¹¹V+ U ¹V¹+ U ¹V¹+ UV¹¹= U¹¹V+2U¹V¹+ UV¹¹;

у¹¹¹= U¹¹¹V+ U¹¹V¹+2U¹¹V¹+2U ¹V¹¹+ U ¹V¹¹+ UV¹¹¹= U¹¹¹V+3U¹¹V¹+3 U¹V¹¹+ UV¹¹¹;

Аналогично получим

у⁽⁴⁾= U⁽⁴⁾V+4 U¹¹¹V¹+6 U¹¹V¹¹+4 U¹V¹¹¹+ UV⁽⁴⁾ и т.д.

Нетрудно заметить, что правые части всех этих формул напоминают разложение степеней бинома U+V, (U+V) ², (U+V) ³ и т.д. Только вместо степеней U и V тут стоят производные соответствующих порядков. Сходство будет особенно полным, если в полученных формулах писать вместо U и V, U⁽⁰⁾ и V⁽⁰⁾, т.е. 0-ые производные от функций U и V (сами функции).

Распространяя этот закон на случай любого n, получим общую формулу

у⁽ⁿ⁾= (UV) ⁽ⁿ⁾ = U⁽ⁿ⁾ V+ n/1! U^(n-1) V ¹+ n( n-1)/2! U^(n-2) V ⁽²⁾+ n( n-1)( n-2)/3! U^(n-3) V ⁽³⁾+…+ n( n-1)…( n-к+1)/К! U^(к) V ^(n-к)+…+ UV⁽ⁿ⁾- формула Лейбница.

Пример: найти (е^хх) ⁽ⁿ⁾

(е^х) ⁽ⁿ⁾=е^х, х¹=1, х¹¹=0 и х⁽ⁿ⁾=0, поэтому (е^хх) ⁽ⁿ⁾= (е^х) ⁽ⁿ⁾х+ n/1! (е^х) ^(n-1)х¹= е^хх+ nе^х=е^х(х+ n).