Формула Тейлора.
Наиболее простыми функциями в смысле вычисления их значений являются многочлены. Поэтому более сложные функции надо уметь представлять, хотя бы приближенно, некоторыми многочленами. Во многих случаях это можно сделать с помощью формулы Тейлора.
Пусть функция ¦(х) имеет все производные до (n +1) порядка включительно в некотором промежутке Х, содержащем т. x0. Найдем многочлен у= Рn(х) степени 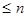 такой, что в т. x0 значения многочлена и функции и всех производных до n-ой включительно – равны в т.x0.
такой, что в т. x0 значения многочлена и функции и всех производных до n-ой включительно – равны в т.x0.
Рn(х) = ¦(х0), Р1n(х0) = ¦1(х0), …, 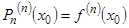 (1)
(1)
Будем искать этот многочлен в виде многочлена по степеням х-x0:
Рn(х) = а0 + а1(х-х0) + а2(х-х0) + … + ап (х-х0)п; (2)
Коэффициенты а0, а1, а2, …, ап – пока неопределенные. Определим эти коэффициенты, чтобы выполнялись условия (1). Производные многочлена имеют вид:
Р1n(х)= а1 + 2а2(х-х0) + 3а3 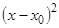 + … + nап (х-х0) n-1;
+ … + nап (х-х0) n-1;
(3) Р11n(х)= 2а2 + 3·2а3(х-х0)+ …+ n (n –1)аn (х-х0)п-2;
Р(n)n(х)= n(n-1)…2 ·1ап
Вычислим Рn(х0), Р1n(х0)… Р(n)n(х0) и приравняем согласно
(1) их ¦(х0), ¦1(х0),… ¦(n)(х0) получим а0= ¦(х0), а1= ¦1(х0), 2а2= ¦11(х0), 3·2а3= ¦111(х0),…, n (n –1)…2·1ап= ¦(n)(х0).
Отсюда имеем а0= ¦(х0), а1= ¦1(х0), а2= ¦11(х0) = ¦11(х0);
1·2 2!
а3= ¦111(х0) , … , ап= ¦(n)(х0) ; (4)
3! n!
Подставим найденные значения коэффициентов а0, …, ап в (2), получим
Pп(х)= ¦(х0) + ¦1(х0) (х-х0)+¦11(х0) 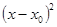 +…+¦(п)(х0) (х-х0)п; (5)
+…+¦(п)(х0) (х-х0)п; (5)
1! 2! n!
По самому построению Рn(х) , Рn(х0)= ¦(х0). В точках же х 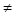 х0, вообще говоря,
х0, вообще говоря, 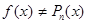 .
.
Обозначим через Rn(х) разность значений данной функции ¦(х) и многочлена Рn(х):
Rn(х)= ¦(х) - Рn(х)
 y
y



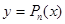



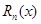
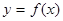
 |
0 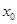
 x
x
Тогда ¦(х)= Рn(х) + Rn(х) или в развернутом виде
¦(х)=¦(х0)+¦1(х0)(х-х0)+¦11(х0)(х-х0)2+…+¦п(х0) (х-х0)п + Rn(х) (6)
1! 2! n!
Формула (6) и есть формула Тейлора для функции ¦(х), а Rn(х)- есть остаточный член формулы.
Она позволяет заменить вычисление значений функции вычислением значений многочлена Рn(х). Отсюда задача: уметь оценивать величину остаточного члена Rn(х) при различных х. Для этого найдем удобную форму выражения остаточного члена.
Запишем Rn(х) в форме Rn(х)= Q(х) (х-х0) п+1 (7), где
(n +1)!
Q(х) – некоторая функция, которую нужно найти.
Формула (6) перепишется
¦(х)= ¦(х0) + (¦1(х0) /1! (х-х0) + (¦11(х0) /2!(х-х0)2 +…+ (¦(п)(х0) / n!(х-х0)п + (Q(х) / (n +1)! (х-х0) п+1. ( 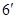 )
)
Возьмем произвольное значение х и зафиксируем его.
Тогда и Q(х) примет определенное значение, обозначим его Q. Рассмотрим вспомогательную функцию от t
(t  [х0, х], х>х0, или t
[х0, х], х>х0, или t  [
[  ,
, 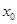 ],
],  <
< 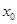 )
)
F(t) = ¦(х)- ¦( t)- ¦1(t) (х- t)- ¦11(t) (х- t)2-…- ¦(п)(t) (х- t)п -Q (х- t)п+1
1! 2! n! (n +1)!
Покажем, что F(t) на [ 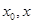 ] удовлетворяет условиям теоремы Ролля.
] удовлетворяет условиям теоремы Ролля.
1) F(t) непрерывна на [х0, х];
2) Найдем производную (х, х0, Q считаем фиксированными)
После всех преобразований получим
F1(t) = ¦(п+1)(t) (х- t)п + Q (х- t)п (8)
n! n!
Значит F1(t) существует на (х0, х).
3) Нетрудно видеть, что F (х0)=0 ( вместо t подставить х0), если учесть выражение (61/ для ¦(х). И, очевидно, F (х)=0 (вместо t подставить х). Но тогда к F(t) на [х0, х] применима теорема Ролля и, значит, найдется точка х0< с< х, что F1(с)=0 или
- ¦(п+1)(с) (х- с)п + Q (х- с)п =0
n! n!
Сокращаем на (х- с)п и получим Q= ¦(п+1)(с).
n!
Подставляя Q в формулу (7),
получаем Rn(х)= ¦(п+1)(с) (х-х0) п+1 (9)
(n +1)!
(9)- есть запись остаточного члена в форме Лагранжа. Т.к. х0< с< х, то можно записать с= х0 + Θ(х-х0), 0< Θ < 1.
И поэтому Rn(х)= ¦(п+1)( х0 + Θ(х-х0)) (х-х0) п+1
(n +1)!
Как видим остаточный член формулы Тейлора (6) похож по виду на остальные члены, но существенное отличие в том, что производная вычисляется не в т.х0, а в некоторой т.c.
Если в частном случае х0=0, то формула Тейлора имеет вид
¦(х)= ¦(0) + ¦1(0) + ¦11(0) х2 + …+ ¦(п)(0) хп + Rn(х) (10)
1! 2! n!
Остаточный член записывается в виде Rn(х)=¦(п+1)(Θх) х п+1 (11)
(n +1)!
(10) с Rn(х) в форме (11) называется формулой Маклорена.
Дата добавления: 2015-10-05; просмотров: 678;
