Теоремы о средних значениях функции.

Теоремами о средних значениях функции называется группа теорем, которая связывает значения функции на концах сегмента со значениями ее производной в промежуточных точках. Эти теоремы играют основную роль во многих теоретических и практических приложениях дифференциального исчисления.

Теорема Ферма (вспомогательная).

Если функция у=¦(х) определена в некотором интервале (a,b)и в какой-либо внутренней точке С этого интервала принимает наибольшее или наименьшее значение, то производная функции в точке С равна 0, если она существует.

Доказательство: Пусть для определенности ¦(с)- есть наибольшее значение функции ¦(х) на (a,b).

Тогда и для любого _Dх>0 и для любого _Dх<0

¦(с + _Dх) £ ¦(с) или ¦(с + _Dх)- ¦(с) £0 (1)

Но тогда ¦(с + _Dх)- ¦(с) £0 при _Dх>0 (1¹)

_Dх

и ¦(с + _Dх)- ¦(с) ³0 при _Dх<0 (1¹¹)

_Dх

т.к. по условию теоремы ¦¹(с) должна существовать, то переходя к пределу в (1¹) и (1¹¹) при _Dх®0, получим

lim_Dх_®0 ¦(с + _Dх)- ¦(с) = ¦¹(с) £0 при _Dх>0

_Dх

и lim_Dх_®0 ¦(с + _Dх)- ¦(с) = ¦¹(с) ³0 при _Dх<0, т.е. ¦¹(с) ³0

_Dх и ¦¹(с) £0

Но эти соотношения выполняются одновременно только при . ч. и т.д.

Теорема Ферма имеет простой геометрический смысл.

Так как производная означает угловой коэффициент касательной к графику, то в точке наибольшего или наименьшего значения функции он равен 0, т.е. касательная параллельна оси ОХ или совпадает с ней.

y

0 a c b x

Теорема Ролля. Если функция :

1). Непрерывна на [a,b];

2). Дифференцируема во всех внутренних точках, т.е. существует у=¦¹(х) на (а,в);

3). Значения функции на концах сигмента равны ¦(а)=¦(в), то между точками а и в найдется хоть одна т. c (а<c<b), в которой производная обращается в нуль: ¦’(с)=0.

Доказательство: По условию функция у=¦(х) непрерывна на [a,b], а поэтому принимает на нем наибольшее и наименьшее значения М и m. Возможны два случая:

1). М = m. Тогда функция у= ¦(х) сохраняет постоянное значение на [a,b], ¦(х)=М=const, значит ¦¹(х)=0, точкой c является любая точка (а,в).

2). М > m, значения М и m не могут приниматься функцией одновременно на концах, ибо ¦(а)=¦(в). Значит, наибольшее М или наименьшее m значения принимаются в некоторой внутренней т.c, а<c<b. Но по теореме Ферма тогда ¦¹(с)=0.

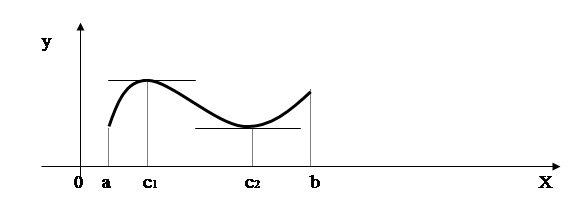
Геометрически теорема Ролля означает следующее:

Если непрерывная кривая изображает график дифференцируемой функции, то между двумя ее точками с одинаковыми ординатами всегда существует т.c, в которой касательная параллельна оси ОХ. Таких точек может быть и несколько. Особенно важный случай теоремы, когда ¦(а)=¦(в)=0. Тогда заключение теоремы звучит так: между двумя корнями функции ¦(х) лежит хоть один корень производной. Корнем функции называют точку, где функция обращается в нуль.

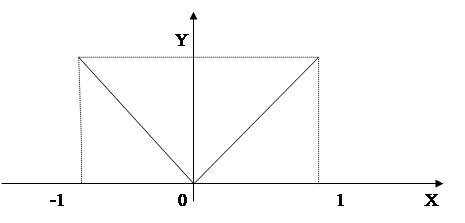
Замечание: Требование существования производной во всех внутренних точках [a,b]существенно. Все условия выполнены, кроме существования производной для 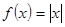на 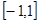и заключение теоремы не выполнимо / в т.0 производной не существует /.

Теорема Лагранжа. Если функция у=¦(х):

1). Непрерывна на [a,b];

2). Дифференцируема во всех внутренних точках, т.е. существует у=¦¹(х) на (а,в), то между точками а и в найдется хоть одна т.c (а<c<b), такая, что для нее выполнимо равенство:

¦(в)-¦(а)= ¦¹(с) (1)

в-а

Доказательство: рассмотрим на [a,b] вспомогательную функцию F (х)= ¦(х)-¦(а)- ¦(в)-¦(а) · (х-а) или F (х)= ¦(х)- ¦(а) - Q(х-а)

в-а

Q

Эта функция на [a,b] удовлетворяет всем условиям теоремы Ролля, т.к. 1).она непрерывна, как сумма непрерывных; 2). Дифференцируема на (а;в): F ¹(х)= ¦¹(х)- Q;

3). Значения на концах равны F (а)= F (в)=0. Действительно F (а)= ¦(а)- ¦(а)- Q(а-а)=0;

F (в)= ¦(в)- ¦(а)- ¦(в)-¦(а)· (в-а)=0

в-а

Но тогда для функции F (х) справедливо и заключение: F ¹(с)=0 или ¦¹(с)- Q=0 или ¦¹(с)= ¦(в)-¦(а) , т.е. (1)

в-а

Формулу (1) часто называют формулой Лагранжа или формулой конечных приращений. Записывают часто в виде

¦(в)-¦(а)= ¦¹(с) (в-а), а<c<b

Геометрический смысл теоремы Лагранжа.

Изобразим на чертеже график функции у=¦(х), удовлетворяющий на [a,b] всем условиям теоремы Лагранжа. Точки А и В соответствуют значениям функции у=¦(х ) на концах сегмента ¦(а) и ¦(в). Соединим т.А и т.В хордой АВ и проведем АС параллельно оси ОХ, угол ВСА= , tgα- угловой коэффициент хорды АВ.

Но tgα= ВС = ¦(в)-¦(а) , т.е. слева в (1) стоит угловой

АС в-а

коэффициент хорды АВ; но ¦¹(с)-

угловой коэффициент касательной к кривой у=¦(х) в точке с абсциссой с. Т.к. эти угловые коэффициенты равны, то касательная в т.М с абсциссой С параллельна хорде АВ.

Итак, геометрически утверждение теоремы Лагранжа равносильно следующему: на графике функции 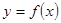, удовлетворяющей условиям 1 и2 теоремы Лагранжа, найдется хоть одна точка М, касательная в которой параллельна хорде АВ, соединяющей концы графика.

Замечание: теорема Ролля- частный случай теоремы Лагранжа, достаточно потребовать ¦(а)=¦(в) и хорда АВ будет параллельна оси ОХ.

Часто применяется другой вид записи формулы Лагранжа:

т.к. а<c<b, то 0<c-a<b-a, но тогда с-а =Θ

в-а

причем 0< Θ<1 или с-а= Θ (в-а).

Тогда с=а+ Θ (в-а), получим

¦(в)- ¦(а)= (в-а) ¦¹[ а+ Θ (в-а)], 0< Θ<1 (2)- приращение функции на сегменте равно произведению производной в некоторой промежуточной точке на приращение независимой переменной.

y

A

Обобщением теоремы Лагранжа является теорема Коши.

Теорема Коши: если функции ¦(х) и q(х) удовлетворяют условиям:

1). ¦(х) и q(х) непрерывны на [а,в];

2). ¦(х) и q(х) дифференцируемы во всех внутренних точках [а,в], т.е. существуют ¦¹(х) и q¹(х) на (а,в);

3). Производная q¹(х) 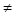0, то

между а и в найдется хоть одна т.c (а<c<b) такая, что для нее выполнимо равенство

¦(в)- ¦(а) = ¦¹(с)

q (в)- q (а) q¹(c) (3) - формула Коши

Доказательство: Заметим, что q (в)- q (а) 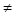0, т.к. иначе было бы q(в)= q (а) и функция q(х) на [а,в] удовлетворила бы условиям теоремы Ролля, а значит в некоторой т. а<c<b q’(с)=0, чего по условию нет. Значит обе части (3) имеют смысл.

Докажем равенство (3).

Рассмотрим вспомогательную функцию

F (х)= ¦(х)-¦(а)- Q [q (х)-q(а)], где

Q= ¦(в)- ¦(а) . На [а,в] F (х) удовлетворяет всем 3-ем условиям

q(в)- q(а)

теоремы Ролля:

1) F (х) непрерывна как алгебраическая сумма непрерывных;

2) F ¹(х)= ¦¹(х)- Q q¹(х) существует на (а,в), т.к. существует ¦¹(х) и q¹(х);

3) F (а)= F (в)=0

Но тогда справедливо и заключение теоремы Ролля, т.е. существует точка а<c<b, что F ¹(с)=0 отсюда ¦¹(с)= ¦(в)- ¦(а) · q¹(с)

q(в)- q(а)

Замечание 1. Теорема Лагранжа получается как частный случай из теоремы Коши при q (х)=х.

Замечание 2. Нельзя доказать теорему Коши простым применением формул Лагранжа к числителю и знаменателю выражения

¦(в)- ¦(а) = ¦¹(с₁)(в-а) = ¦¹(с₁)

q(в)- q(а) q ¹(с₂)(в-а) q ¹(с₂)

точки c₁ и c₂ не совпадают и их общее значение c ниоткуда не следует при этом доказательстве.