Взаимно обратные функции в традиционных обозначениях аргумента и функции
Часто бывает так, что функция, являющаяся обратной к другой функции, имеет самостоятельное значение и поэтому её аргумент традиционно обозначается через x, а функция через y. Например, известно, что функции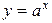 
и 
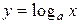являются взаимно обратными; то же относительно функци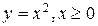й 
и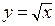 
. В этом случае прямая и обратная функция записываются в следующем виде:
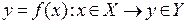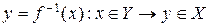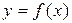и 
.
|
|
и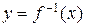 
не совпадают друг с другом, но имеют осевую симметрию относительно прямой y = x - биссектрисы первого и третьего координатных углов. На рисунке 58 приведены пары взаимно обратных функций и их графики.
| 
|
Рис. 58
Очевидно, что взаимно обратные функции «гасят» друг друга, но только на множестве тех значений аргумента, для которых соблюдается биективность отображений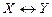 
.
Например, 1)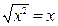 
только при 
, 
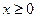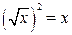только при ;
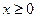2) 
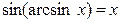только при 
, 
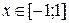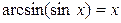только при 
;
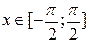3) 
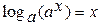при 
, 
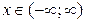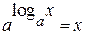только при 
;
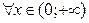4) 
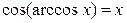при , 
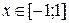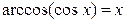только при 
.
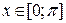Дата добавления: 2015-10-19; просмотров: 1244;