Определение обратной функции

Рассмотрим числовую функцию y = f(x): 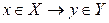, причем отображение множества X на множество Y , описываемое этой функцией, является биективным, (рис. 57).

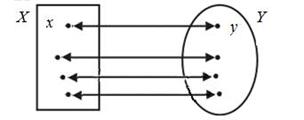Рис. 57

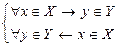
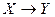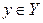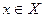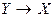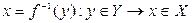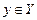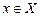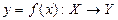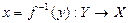Так как отображение является взаимно однозначным (биективным), то каждое значение является образом единственного значения ; поэтому может быть рассмотрено обратное отображение или обратная функция, которая обозначается и ставит в соответствие каждому значению единственное значение . При этом обратная функция описывает также биективное отображение. Обе функции и называются взаимно обратными функциями. Таким образом, необходимым и достаточным условием для существования обратной функции является биективность отображения, описываемого данной функцией.