Монотонность и локальные экстремумы функции
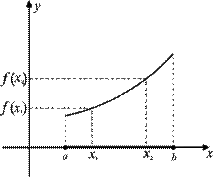
Функция 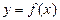 называется монотонно возрастающей функцией на промежутке
называется монотонно возрастающей функцией на промежутке 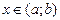 , если любому большему значению аргумента из этого промежутка соответствует большее значение функции, (рис.52).
, если любому большему значению аргумента из этого промежутка соответствует большее значение функции, (рис.52).
| 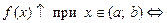
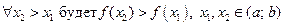
|
Рис.52
Функция 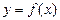 называется монотонно убывающей функцией на промежутке
называется монотонно убывающей функцией на промежутке 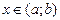 , если любому большему значению аргумента из этого промежутка соответствует меньшее значение функции, (рис.53).
, если любому большему значению аргумента из этого промежутка соответствует меньшее значение функции, (рис.53).
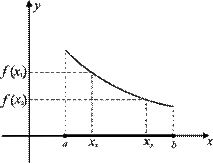 Рис.53 Рис.53
| 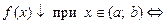
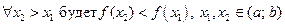
|
Функция f(x) на промежутке 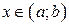 называется монотонной функцией, если она на этом промежутке только монотонно возрастает или только монотонно убывает.
называется монотонной функцией, если она на этом промежутке только монотонно возрастает или только монотонно убывает.
Точка 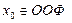
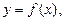
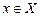 называется точкой локального максимума функции, если значение функции в этой точке является наибольшим по сравнению с теми значениями, которые функция имеет во всех точках, достаточно близких к точке
называется точкой локального максимума функции, если значение функции в этой точке является наибольшим по сравнению с теми значениями, которые функция имеет во всех точках, достаточно близких к точке 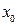 .
.
Максимумом функции 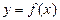 называется значение функции в её точке локального максимума, (рис.54).
называется значение функции в её точке локального максимума, (рис.54).
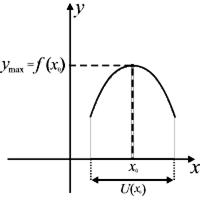
| 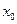 – точка локального максимума функции – точка локального максимума функции 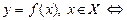 существует такая окрестность
существует такая окрестность 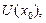 что что 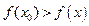 при при 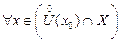 ; ;
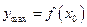
|
Рис.54
Точка 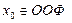
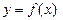 ,
, 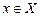 называется точкой локального минимума функции, если значение функции в этой точке является наименьшим по сравнению с теми значениями, которые функция имеет во всех точках, достаточно близких к точке
называется точкой локального минимума функции, если значение функции в этой точке является наименьшим по сравнению с теми значениями, которые функция имеет во всех точках, достаточно близких к точке 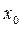 .
.
Минимумом функции 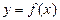 называется значение функции в её точке локального минимума, (рис. 55).
называется значение функции в её точке локального минимума, (рис. 55). 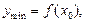 где
где 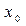 - точка минимума.
- точка минимума.
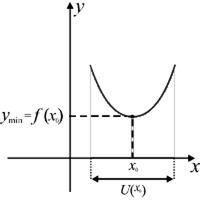
| 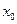 – точка локального минимума функции – точка локального минимума функции 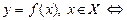 существует такая окрестность
существует такая окрестность 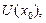 что что 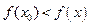 при при 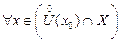 ; ;
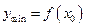
|
Рис.55
Локальные максимумы и минимумы функции называются локальными экстремумами функции. Функция может иметь на своей ООФ несколько локальных экстремумов (и даже бесконечно много). Локальные экстремумы могут быть только во внутренних точках ООФ, так как в их определении участвуют окрестности точек.
Если имеется график функции, то промежутки её монотонности и локальные экстремумы определяются визуально.
Например, рассмотрим функцию 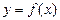 , заданную своим графиком и по графику охарактеризуем ее монотонность и экстремумы (рис.56):
, заданную своим графиком и по графику охарактеризуем ее монотонность и экстремумы (рис.56):
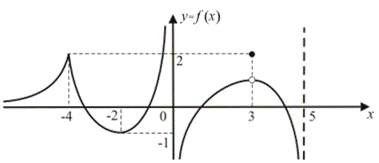
Рис.56
ООФ: 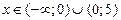 ;
;
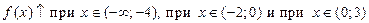 ;
;
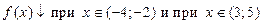 ;
;
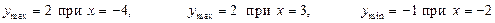 .
.
Если функция задана аналитически и является непрерывной и дифференцируемой, то промежутки ее монотонности и локальные экстремумы можно найти с помощью необходимых и достаточных условий для этих характеристик, которые будут рассмотрены в теме «Дифференциальное исчисление функций одной переменной».
Замечание (к понятиям монотонности и локальных экстремумов)
Все определенные здесь понятия монотонности и локальных экстремумов функции предполагают строгие неравенства для значений функции, поэтому часто называются строгой монотонностью и строгими локальными экстремумами:
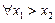 верно
верно 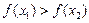 (или
(или 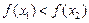 )
) 
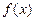 строго
строго 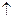 (или строго
(или строго 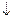 );
);
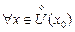 верно
верно 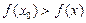 (или
(или 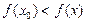 )
) 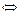
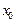 - точка строгого локального максимума (или строгого локального минимума).
- точка строгого локального максимума (или строгого локального минимума).
В учебной литературе можно встретить определения аналогичных нестрогих понятий:
если 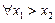 ,
, 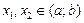 верно
верно 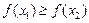 , то
, то 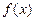 называется неубывающей функциейна промежутке
называется неубывающей функциейна промежутке 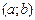 , или нестрого возрастающей;
, или нестрого возрастающей;
если 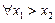 ,
, 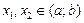 верно
верно 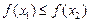 , то
, то 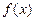 называется невозрастающей функциейна промежутке
называется невозрастающей функциейна промежутке 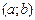 , или нестрого убывающей;
, или нестрого убывающей;
если 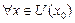 верно
верно 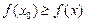 (или
(или 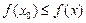 ), то точка
), то точка 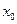 азывается точкой нестрогого локального экстремумафункции f(x)(нестрогого максимума или нестрого минимума).
азывается точкой нестрогого локального экстремумафункции f(x)(нестрогого максимума или нестрого минимума).
Далее по умолчанию будем понимать монотонность и экстремумы как строгие понятия.
Дата добавления: 2015-10-19; просмотров: 2040;
