Нули функции и промежутки знакопостоянства
Нулем функции 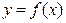 называется такое значение
называется такое значение 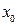 ее аргумента, при котором значение функции равно нулю:
ее аргумента, при котором значение функции равно нулю: 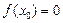 .
.
Множество нулей функции 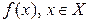 – это следующее множество:
– это следующее множество:
 .
.
Промежутком знакопостоянства функции 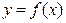 называется множество значений ее аргумента, входящий в ООФ, во всех точках которого функция принимает значения одного знака:
называется множество значений ее аргумента, входящий в ООФ, во всех точках которого функция принимает значения одного знака:  или
или  .
.
Промежутки знакопостоянства функции 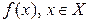 обозначаются следующим образом:
обозначаются следующим образом:
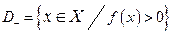 ,
, 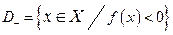 .
.
Пример (нули и промежутки знакопостоянства функции)
Найти множество нулей и промежутки знакопостоянства заданных функций:
1)  2)
2) 
Решение
1) 
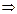 ООФ:
ООФ:  ;
;
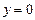
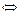
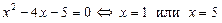
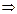
данная функция имеет два нуля, которые разбивают ее ООФ на промежутки знакопостоянства функции:

знак функции на каждом из обозначенных промежутков можно определить по одной точке – представительнице промежутка, если вычислить знак значения функции в этой точке:

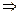
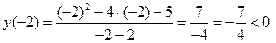
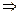
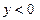 при
при 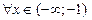 ;
;

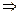
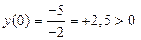
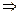
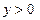 при
при 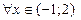 ;
;
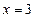
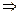


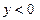 при
при  ;
;
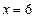
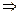

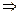
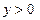 при
при 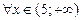 ;
;
Таким образом, получено, что 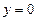 при
при 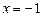 или
или 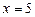 ;
;
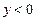 при
при 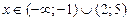 ;
;  при
при 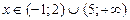 ;
;
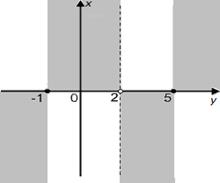
Нули функции и промежутки ее знакопостоянства вместе с ООФ дают первичную информацию о расположении графика функции на координатной плоскости  :
:
точки  и и 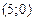 принадлежат графику;
прямая принадлежат графику;
прямая 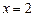 графиком не пересекается;
график будет расположен
выше оси графиком не пересекается;
график будет расположен
выше оси 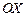 при при  и и  ,
ниже оси ,
ниже оси 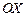 при при 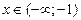 и и 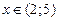 . .
| 
|
2) 
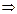 ООФ:
ООФ: 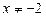 ;
;
 , следовательно, функция имеет два нуля;
, следовательно, функция имеет два нуля;
промежутки знакопостоянства функции:
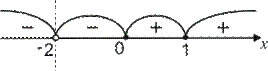
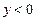 при
при  ;
;  при
при  .
.
Ответ:
1) 
2) 
Дата добавления: 2015-10-19; просмотров: 3684;
